- 平成29年改訂学習指導要領における算数科・数学科の「見方・考え方」とは,どのようなものでしょうか。
- 算数科・数学科の特質に応じた見方・考え方は,数学的な見方・考え方です。
小学校では「事象を,数量や図形及びそれらの関係などに着目して捉え,統合的・発展的に考えること」,中学校では「…論理的,統合的・発展的に考えること」,高等学校では「…論理的,統合的・発展的,体系的に考えること」です。
数学的な見方:「事象を数量や図形及びそれらの関係についての概念等に着目してその特徴や本質を捉えること」小・中・高共通
数学的な考え方:「目的に応じて数,式,図,表,グラフ等を活用しつつ,」
小「根拠を基に筋道を立てて考え,問題解決の過程を振り返るなどして既習の知識及び技能等を関連付けながら,統合的・発展的に考えること」
中「論理的に考え,問題解決の過程を振り返るなどして既習の知識及び技能を関連付けながら,統合的・発展的に考えること」
高「論理的に考え,問題解決の過程を振り返るなどして既習の知識及び技能を関連付けながら,統合的・発展的に考えたり,体系的に考えたりすること」
1 学びの中核「見方・考え方」
(1)深い学びの鍵
平成29年改訂学習指導要領では,「見方・考え方」が,各教科等を学ぶ本質的な意義の中核をなすものとして改めて明示されました。
今回の改訂で各教科等の目標に位置付けられた見方・考え方は,各教科等の特質に応じた,各教科等ならではの物事を捉える視点や考え方です。
この見方・考え方を働かせることができれば,次のような姿を見ることができます。
・ 新しい知識・技能を,既にもっている知識・技能と結び付けながら社会の中で生きて働くものとして習得できる
・ 思考力・判断力・表現力を豊かなものにできる
・ 社会や世界にどのように関わるかの視座を形成できる
また,既に身に付けた資質・能力の三つの柱によって支えられた見方・考え方が,習得・活用・探究という学びの過程の中で働くことを通じて,資質・能力がさらに伸ばされたり,新たな資質・能力が育まれたりし,それによって見方・考え方が更に豊かなものになる,という相互の関係にあります。
このような見方・考え方を働かせた学習は,アクティブ・ラーニングの視点からの学びである「主体的・対話的で深い学び」の実現につながります。見方・考え方は深い学びを実現する鍵となります。
(2)捉え方の豊かさ
「見方・考え方」には,各教科等に応じた特質があります。
小学校社会科
例えば,小学校社会科では,社会的な見方・考え方を働かせ,課題を追究したり解決したりする活動を通して,グローバル化する国際社会に主体的に生きる平和で民主的な国家及び社会の形成者に必要な公民としての資質・能力の基礎を育成します。
位置や空間的な広がり,時期や時間の経過,事象や人々の相互関係などに着目して社会的事象を捉え,
比較・分類したり総合したり,地域の人々や国民の生活と関連付けたりする
小学校算数科
また,算数科では,数学的な見方・考え方を働かせ深い学びを実現し,数学的活動を通して数学的に考える資質・能力の育成を図ります。
事象を数量や図形及びそれらの関係などに着目して捉え,
根拠を基に筋道を立てて考え,統合的・発展的に考える
小学校音楽科
音楽科では,以下のような音楽的な見方・考え方を働かせ深い学びを実現し,多様な音楽活動を通して資質・能力の育成を図ります。
音楽に対する感性を働かせ,音や音楽を,音楽を形づくっている要素とその働きの視点で捉え,
自己のイメージや感情,生活や文化などと関連付ける
このように,見方・考え方には教科等の特質があります。見方・考え方は,対象の捉え方,アプローチの仕方と言えます。
まずは物事をどのように捉えるか。まさに,国語の目,理科の目,美術の目など多様であるほど,多面的多角的に捉えられます。
そして何より対象を一面的ではなく,より豊かに捉えられると言うことです。
では,対象を算数・数学の目で捉えるとどのように見えるのでしょうか。
(3)ピタゴラスの捉えたもの
算数・数学の目というのは,このように対象を,数の目,量の目,図形の目などで捉えることです。そこから数学的な思考が始まります。
 図形の目といえば,ピタゴラスのエピソードが思い浮かびます。
図形の目といえば,ピタゴラスのエピソードが思い浮かびます。
ピタゴラスは,ある寺院に入ったとき,床のタイルの模様に目がとまりました。
その模様を見て考える中で,三平方の定理を発見したと伝えられます。
何の変哲も無いタイルです。寺院の建築や環境・自然の美しさを捉えるか,歴史を捉えるか,そこで集う人々を捉えるか,聞こえてくる音や言葉を捉えるか,様々な捉え方があるでしょう。
ピタゴラスは,床のタイルを図形の目で見ていました。
まさに,図形や構成要素,それらの関係などに着目して捉える数学的な見方・考え方です。
2 数学的な見方・考え方とは
(1)教育課程部会の資料から
教育課程部会算数・数学ワーキンググループ(第8回)配付資料(H28.5.24)では,「数学的な見方・考え方」を次のように説明しています。
数学的な見方・考え方とは,事象を数量や図形及びそれらの関係などに着目して捉え,論理的,統合的・発展的に考えること
数学的な見方・考え方では,「事象を数量や図形及びそれらの関係などに着目して捉え」が「数学的な見方」であり,「論理的,統合的・発展的に考える」が「数学的な考え方」であると捉えられます。
小学校算数科,中学校・高等学校数学科では,数学的な見方である「事象を数量や図形及びそれらの関係などに着目して捉える」ことは,質の違いはあるが表現は共通します。
数学的な考え方については,各学校段階で,小学校では「根拠を基に筋道を立てて考え,統合的・発展的に考える」ことから始まり,中学校では「論理的,統合的・発展的に考える」こととなり,高等学校では「論理的,統合的・発展的,体系的に考える」ことへと高まります。
このように,数学的な見方・考え方は,小学校から高等学校へと学習を積み重ねることで,高次な数学的な見方・考え方へ向かいます。
| 見方 | 考え方 | |
|---|---|---|
| 小学校算数 | 事象を数量や図形及びそれらの関係などに着目して捉え, | 根拠を基に筋道を立てて考え,統合的・発展的に考えること |
| 中学校数学 | 事象を数量や図形及びそれらの関係などに着目して捉え, | 論理的,統合的・発展的に考えること |
| 高等学校数学 | 事象を数量や図形及びそれらの関係などに着目して捉え, | 論理的,統合的・発展的,体系的に考えること |
具体的には,以下のようです。
数学的な見方である事象を数量や図形及びそれらの関係などに着目して捉えることについては,
・ 数に着目する
・ 数で表現する
・ 量に着目する
・ 図形に着目する
・ 数量や図形の関係に着目する
数学的な考え方である論理的に考えることについては,
・ 帰納的に考える
・ 順序よく考える
・ 根拠を明らかにする
統合的に考えることについては,
・ 関連づける
・ 既習の事柄と結びつける
発展的に考えることについては,
・ 適用範囲を広げる
・ 条件を変える
・ 新たな視点から捉え直す
などが考えられ,これらが具体的な数学的な見方・考え方です。
※ 文部科学省 教育課程部会算数・数学ワーキンググループ(第8回)配付資料参考資料2P1,2「数学的な見方・考え方」H28.5.24[ONLINE]http://www.mext.go.jp/b_menu/shingi/chukyo/chukyo3/073/siryo/__icsFiles/afieldfile/2016/06/21/1372244_12.pdf(参照2017/05/14)
(2)平成29,30年改訂学習指導要領から
小学校算数科及び中・高等学校数学科で育成を目指す資質・能力の三つの柱を含む目標が明確化にされたことにより,「数学的な見方・考え方」は,それを働かせ,数学的活動を通して,資質・能力を育成する指導原理の構成要素となりました。
「数学的な見方・考え方」は,算数・数学の学習において,どのような視点で物事を捉え,どのような考え方で思考をしていくのかという,物事の特徴や本質を捉える視点や,思考の進め方や方向性を与えます。「数学的な見方・考え方」は,数学的に考える資質・能力を支え方向付けるものであり,算数の学習が創造的に行われるために欠かせません。
また,児童・生徒一人一人が目的意識をもって問題解決に取り組む際に積極的に働かせていくものです。
その意味で「数学的な見方・考え方」は,数学的に考える資質・能力の三つの柱である「知識及び技能」,「思考力,判断力,表現力等」及び「学びに向かう力,人間性等」の全てに対して働かせるものとなります。
そして,算数・数学の学習を通じて,「数学的な見方・考え方」がさらに豊かで確かなものとなっていくと考えられます。
① 小学校算数
小学校学習指導要領解説算数編では,「数学的な見方」及び「数学的な考え方」を次のように解説します。※青字は中学校との違い
数学的な見方
・ 事象を数量や図形及びそれらの関係についての概念等に着目してその特徴や本質を捉えること
数学的な考え方
・ 目的に応じて数,式,図,表,グラフ等を活用し,根拠を基に筋道を立てて考え,問題解決の過程を振り返るなどして既習の知識及び技能等を関連付けながら統合的・発展的に考えること
これらから,算数科の「数学的な見方・考え方」は,次のように整理できます。
事象を,数量や図形及びそれらの関係などに着目して捉え,根拠を基に筋道を立てて考え,統合的・発展的に考えること
※ 文部科学省「小学校学習指導要領(平成 29 年告示)解説 第2章 算数科の目標及び内容 第1節 算数科の目標 1 教科の目標」平成29年7月[ONLINE]https://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2019/03/18/1387017_004.pdf(参照2020-06-12)
② 中学校数学
中学校学習指導要領解説数学編では,「数学的な見方」及び「数学的な考え方」を次のように解説しています。※青字は小学校との違い
数学的な見方
事象を数量や図形及びそれらの関係についての概念等に着目してその特徴や本質を捉えること
数学的な考え方
目的に応じて数,式,図,表,グラフ等を活用しつつ,論理的に考え,問題解決の過程を振り返るなどして既習の知識及び技能を関連付けながら,統合的・発展的に考えること
これらから,中学校数学科の「数学的な見方・考え方」は,次のように整理できます。
事象を,数量や図形及びそれらの関係などに着目して捉え,論理的,統合的・発展的に考えること
※ 文部科学省「中学校学習指導要領(平成 29 年告示)解説 第2章 数学科の目標及び内容 第1節 数学科の目標 1 教科の目標」平成29年6月[ONLINE]https://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2019/03/18/1387018_004.pdf(参照2020-06-12)
③ 高等学校数学
高等学校学習指導要領(平成30年告示)解説数学編では,「数学的な見方」及び「数学的な考え方」を次のように解説します。※青字は中学校との違い
数学的な見方
事象を数量や図形及びそれらの関係についての概念等に着目してその特徴や本質を捉えること
数学的な考え方
目的に応じて数,式,図,表,グラフ等を活用しつつ,論理的に考え,問題解決の過程を振り返るなどして既習の知識及び技能を関連付けながら,統合的・発展的に考えたり,体系的に考えたりすること
これらから,高等学校数学科の「数学的な見方・考え方」は,次のように整理できます。
事象を,数量や図形及びそれらの関係などに着目して捉え,論理的,統合的・発展的,体系的に考えること
※ 文部科学省「高等学校学習指導要領(平成30年告示)解説数学編」[ONLINE]https://www.mext.go.jp/content/1407073_05_1_2.pdf(cf.2020-06-12)
④ 統合的・発展的に考える
「統合的・発展的に考える」ことは,今回の学習指導要領の改訂で重視されています。
小学校算数科では,次のようです。
統合的に考察する
・ 異なる複数の事柄をある観点から捉え,それらに 共通点を見いだして一つのものとして捉え直すこと
発展的に考察する
・ 物事を固定的なもの,確定的なものと考えず,絶えず考察の範囲を広げていくことで新しい知識や理解を得ようと すること
中学校・高等学校数学科では,次のようです。
統合的に考える
・ 既習のものと新しく生み出したものとを包括的に扱えるように意味を規定したり,処理の仕方をまとめたりすること
発展的に考える
・ 数学を既成のものとみなしたり,固定的で確定的なものとみなしたりせず,新たな概念,原理や法則などを創造しようとすること
算数・数学科の学習では,このように創造的な発展を図るとともに,創造したものをより高い,あるいは,より広い観点から統合してみられるようにすることが大切です。
3 数学的な見方・考え方の具体
数学的な見方・考え方の具体は,平成29年改訂学習指導要領の「思考力,判断力,表現力等」の指導内容に示されています。
目標や内容を,資質・能力の三つの柱に基づき共通化して構成していることから,数学的な見方・考え方の具体は,領域や学年,校種間の縦横に対応させた指導内容から捉えることができます。
(1)枠組みや構成を共通化
平成29年改訂学習指導要領は,全体像を分かりやすく見渡せるよう学びの地図として枠組みが大きく見直されました。
それにより,教科の目標や学年の目標をはじめ指導内容などについても統一して整理されました。
① 目標の構成
教科等の目標は,下の図のように冒頭部分の柱書と箇条書き部分の資質・能力の三つの柱で構成されています。
「思考力,判断力,表現力等」は,資質・能力の三つの柱の2番目に位置付けられています。
教科等の目標の構成
○ 柱書(冒頭部分)
1. 「…見方・考え方を働かせて」:教科等の特質
2. 「…活動を通して」:主体的・対話的で深い学びの学習過程,学習活動
3. 「…資質・能力…育成を目指す」:育成を目指す資質・能力
○ 三つの柱(箇条書き部分) 育成を目指す資質・能力の具体
(1) 知識・技能
(2) 思考力・判断力・表現力等
(3) 学びに向かう力・人間性等
学年の目標は,教科等の目標に準じて,(1)「知識・技能」(2)「思考力・判断力・表現力等」(3)「学びに向かう力・人間性等」の資質・能力の三つの柱で構成されています。
【教科等の目標】学習指導要領における「教科等の目標」の構造はこのようになっている
【算数科・数学科の目標の系統】算数・数学科「教科・学年の目標」と高等学校数学科「教科・科目の目標」を一覧する
② 指導内容の構成
指導内容についても構造化されています。
平成29年改訂学習指導要領では,身に付ける「知識及び技能」と「思考力,判断力,表現力等」を別項で明記しています。
・ 「知識及び技能」は,「ア 次のような知識及び技能を身に付けること。」
・ 「思考力,判断力,表現力等」は,「イ 次のような思考力,判断力,表現力等を身に付けること。」
として指導内容を示しています。
下は,小学校算数科第1学年の指導内容の記述です。
第2 各学年の目標及び内容 〔第1学年〕2内容 A 数と計算
(1) 数の構成と表し方に関わる数学的活動を通して,次の事項を身に付けることができるよう指導する。
ア 次のような知識及び技能を身に付けること。
(ア) ものとものとを対応させることによって,ものの個数を比べること。
(イ) 個数や順番を正しく数えたり表したりすること。
(ウ) 数の大小や順序を考えることによって,数の系列を作ったり,数直線の上に表したりすること。
(エ) 一つの数をほかの数の和や差としてみるなど,ほかの数と関係付けてみること。
(オ) 2位数の表し方について理解すること。
(カ) 簡単な場合について,3位数の表し方を知ること。
(キ) 数を,十を単位としてみること。
(ク) 具体物をまとめて数えたり等分したりして整理し,表すこと。
イ 次のような思考力,判断力,表現力等を身に付けること。
(ア) 数のまとまりに着目し,数の大きさの比べ方や数え方を考え,それらを日常生活に生かすこと。
この構成は,中学校数学科も同様です。
第2 各学年の目標及び内容 〔第1学年〕2内容 A 数と式
(1) 正の数と負の数について,数学的活動を通して,次の事項を身に付けることができるよう指導する。
ア 次のような知識及び技能を身に付けること。
(ア) 正の数と負の数の必要性と意味を理解すること。
(イ) 正の数と負の数の四則計算をすること。
(ウ) 具体的な場面で正の数と負の数を用いて表したり処理したりすること。
イ 次のような思考力,判断力,表現力等を身に付けること。
(ア) 算数で学習した数の四則計算と関連付けて,正の数と負の数の四則計算の方法を考察し表現すること。
(イ) 正の数と負の数を具体的な場面で活用すること。
また,高等学校数学科でも同様の構成で内容が示されています。
第1 数学I 2内容
(1) 数と式 数と式について,数学的活動を通して,次の事項を身に付けることができるよう指導する。
ア 次のような知識及び技能を身に付けること。
(ア) 数を実数まで拡張する意義を理解し,簡単な無理数の四則計算をすること。
(イ) 集合と命題に関する基本的な概念を理解すること。
(ウ) 二次の乗法公式及び因数分解の公式の理解を深めること。
(エ) 不等式の解の意味や不等式の性質について理解し,一次不等式の解を求めること。
イ 次のような思考力,判断力,表現力等を身に付けること。
(ア) 集合の考えを用いて論理的に考察し,簡単な命題を証明すること。
(イ) 問題を解決する際に,既に学習した計算の方法と関連付けて,式を多面的に捉えたり目的に応じて適切に変形したりすること。
(ウ) 不等式の性質を基に一次不等式を解く方法を考察すること。
(エ) 日常の事象や社会の事象などを数学的に捉え,一次不等式を問題解決に活用すること。
③ 「思考力,判断力,表現力等」で示す具体
このように,平成29年改訂学習指導要領では,「思考力,判断力,表現力等」の指導内容は,資質・能力の三つの柱に基づいて統一して明示されています。
数学的な見方・考え方の具体については,「思考力,判断力,表現力等」の指導内容に含めて示されます。
例えば,以下は先に述べた小学校算数科第1学年「A 数と計算」の指導内容の一部です。
イ 次のような思考力,判断力,表現力等を身に付けること。
(ア) 数のまとまりに着目し,数の大きさの比べ方や数え方を考え,それらを日常生活に生かすこと。
このうち「数のまとまりに着目し」が数学的な見方であり,「数の大きさの比べ方や数え方を考え」が数学的な考え方です。このような指導内容の記述から,内容に応じた数学的な見方・考え方の具体を捉えることができます。
※ここには,判断力や表現力が含まれます。「日常生活に生かす」ときにも数学的な見方・考え方は発揮されます。
(2)「数と計算」の具体例
「思考力,判断力,表現力等」の内容は,「イ 次のような思考力,判断力,表現力等を身に付けること」の指導内容の部分に示されます。数学的な見方・考え方の具体を見出すため,例として小学校算数科「A 数と計算」及び中学校数学科「A 数と計算」の「思考力,判断力,表現力等」に関わる指導内容を以下に示します。
| 小 | A 数と計算 |
|---|---|
| 第1学年 | ・数のまとまりに着目し,数の大きさの比べ方や数え方を考え,それらを日常生活に生かすこと。 ・数量の関係に着目し,計算の意味や計算の仕方を考えたり,日常生活に生かしたりすること。 |
| 第2学年 | ・数のまとまりに着目し,大きな数の大きさの比べ方や数え方を考え,日常生活に生かすこと。 ・数量の関係に着目し,計算の意味や計算の仕方を考えたり計算に関して成り立つ性質を見いだしたりするとともに,その性質を活用して,計算を工夫したり計算の確かめをしたりすること。 ・数量の関係に着目し,計算を日常生活に生かすこと。 |
| 第3学年 | ・数のまとまりに着目し,大きな数の大きさの比べ方や表し方を考え,日常生活に生かすこと。 ・数量の関係に着目し,計算の仕方を考えたり計算に関して成り立つ性質を見いだしたりするとともに,その性質を活用して,計算を工夫したり計算の確かめをしたりすること。 ・数量の関係に着目し,計算の意味や計算の仕方を考えたり,計算に関して成り立つ性質を見いだしたりするとともに,その性質を活用して,計算を工夫したり計算の確かめをしたりすること。 ・数量の関係に着目し,計算を日常生活に生かすこと。 ・数のまとまりに着目し,小数や分数でも数の大きさを比べたり計算したりできるかどうかを考えるとともに,小数や分数を日常生活に生かすこと。 ・数量の関係に着目し,数量の関係を図や式を用いて簡潔に表したり,式と図を関連付けて式を読んだりすること。 ・そろばんの仕組みに着目し,大きな数や小数の計算の仕方を考えること。 |
| 小 | A 数と計算 |
| 第4学年 | ・数のまとまりに着目し,大きな数の大きさの比べ方や表し方を統合的に捉えるとともに,それらを日常生活に生かすこと。 ・日常の事象における場面に着目し,目的に合った数の処理の仕方を考えるとともに,それを日常生活に生かすこと。 ・数量の関係に着目し,計算の仕方を考えたり計算に関して成り立つ性質を見いだしたりするとともに,その性質を活用して,計算を工夫したり計算の確かめをしたりすること。 ・数の表し方の仕組みや数を構成する単位に着目し,計算の仕方を考えるとともに,それを日常生活に生かすこと。 ・数を構成する単位に着目し,大きさの等しい分数を探したり,計算の仕方を考えたりするとともに,それを日常生活に生かすこと。 ・問題場面の数量の関係に着目し,数量の関係を簡潔に,また一般的に表現したり,式の意味を読み取ったりすること。 ・数量の関係に着目し,計算に関して成り立つ性質を用いて計算の仕方を考えること。 ・そろばんの仕組みに着目し,大きな数や小数の計算の仕方を考えること。 |
| 第5学年 | ・乗法及び除法に着目し,観点を決めて整数を類別する仕方を考えたり,数の構成について考察したりするとともに,日常生活に生かすこと。 ・数の表し方の仕組みに着目し,数の相対的な大きさを考察し,計算などに有効に生かすこと。 ・乗法及び除法の意味に着目し,乗数や除数が小数である場合まで数の範囲を広げて乗法及び除法の意味を捉え直すとともに,それらの計算の仕方を考えたり,それらを日常生活に生かしたりすること。 ・数を構成する単位に着目し,数の相等及び大小関係について考察すること。 ・分数の表現に着目し,除法の結果の表し方を振り返り,分数の意味をまとめること。 ・分数の意味や表現に着目し,計算の仕方を考えること。 ・二つの数量の対応や変わり方に着目し,簡単な式で表されている関係について考察すること。 |
| 第6学年 | ・数の意味と表現,計算について成り立つ性質に着目し,計算の仕方を多面的に捉え考えること。 ・問題場面の数量の関係に着目し,数量の関係を簡潔かつ一般的に表現したり,式の意味を読み取ったりすること。 |
| 中 | A 数と式 |
| 第1学年 | ・算数で学習した数の四則計算と関連付けて,正の数と負の数の四則計算の方法を考察し表現すること。 ・正の数と負の数を具体的な場面で活用すること。 ・具体的な場面と関連付けて,一次式の加法と減法の計算の方法を考察し表現すること。 ・等式の性質を基にして,一元一次方程式を解く方法を考察し表現すること。 ・一元一次方程式を具体的な場面で活用すること。 |
| 第2学年 | ・具体的な数の計算や既に学習した計算の方法と関連付けて,整式の加法と減法及び単項式の乗法と除法の計算の方法を考察し表現すること。 ・文字を用いた式を具体的な場面で活用すること。 ・一元一次方程式と関連付けて,連立二元一次方程式を解く方法を考察し表現すること。 ・連立二元一次方程式を具体的な場面で活用すること。 |
| 第3学年 | ・既に学習した計算の方法と関連付けて,数の平方根を含む式の計算の方法を考察し表現すること。 ・数の平方根を具体的な場面で活用すること。 ・既に学習した計算の方法と関連付けて,式の展開や因数分解をする方法を考察し表現すること。 ・文字を用いた式で数量及び数量の関係を捉え説明すること。 ・因数分解や平方根の考えを基にして,二次方程式を解く方法を考察し表現すること。 ・二次方程式を具体的な場面で活用すること。 |
これらの指導内容から,内容に応じた具体的な数学的な見方・考え方を捉えることができます。
例えば,小学校第4学年算数科「A 数と計算」では,「数のまとまりに着目し」,「日常の事象における場面に着目し」などが数学的な見方です。
したがって,第4学年「A 数と計算」領域では,以下の視点に着目する数学的な見方を育成する必要があります。
・ 数のまとまり
・ 日常の事象における場面
・ 数量の関係
・ 数の表し方の仕組みや数を構成する単位
・ 数を構成する単位
・ 問題場面の数量の関係
・ そろばんの仕組み
(3)領域ごとの特徴
以下の表は,平成29年改訂学習指導要領に示される小学校算数科・中学校数学科の領域別「思考力,判断力,表現力等」 です。ここから,領域の指導内容に応じた特徴的な数学的な見方や数学的な考え方を読み取ることができます。「〜に着目し」に当たる部分は「数学的な見方」,「〜考える」「〜捉える」などに当たる部分は「数学的な考え方」と考えられます。
| 小 | A 数と計算 | B 図 形 | C 測 定 | D データの活用 | |
|---|---|---|---|---|---|
| 第1学年 | ものの数に着目し,具体物や図などを用いて数の数え方や計算の仕方を考える力 | ものの形に着目して特徴を捉えたり,具体的な操作を通して形の構成について考えたりする力 | 身の回りにあるものの特徴を量に着目して捉え,量の大きさの比べ方を考える力 | データの個数に着目して身の回りの事象の特徴を捉える力 | |
| 第2学年 | 数とその表現や数量の関係に着目し,必要に応じて具体物や図などを用いて数の表し方や計算の仕方などを考察する力 | 平面図形の特徴を図形を構成する要素に着目して捉えたり,身の回りの事象を図形の性質から考察したりする力 | 身の回りにあるものの特徴を量に着目して捉え,量の単位を用いて的確に表現する力 | 身の回りの事象をデータの特徴に着目して捉え,簡潔に表現したり考察したりする力 | |
| 第3学年 | 数とその表現や数量の関係に着目し,必要に応じて具体物や図などを用いて数の表し方や計算の仕方などを考察する力 | 平面図形の特徴を図形を構成する要素に着目して捉えたり,身の回りの事象を図形の性質から考察したりする力 | 身の回りにあるものの特徴を量に着目して捉え,量の単位を用いて的確に表現する力 | 身の回りの事象をデータの特徴に着目して捉え,簡潔に表現したり適切に判断したりする力 | |
| 小 | A 数と計算 | B 図 形 | C 変化と関係 | D データの活用 | |
| 第4学年 | 数とその表現や数量の関係に着目し,目的に合った表現方法を用いて計算の仕方などを考察する力 | 図形を構成する要素及びそれらの位置関係に着目し,図形の性質や図形の計量について考察する力 | 伴って変わる二つの数量やそれらの関係に着目し,変化や対応の特徴を見いだして,二つの数量の関係を表や式を用いて考察する力 | 目的に応じてデータを収集し,データの特徴や傾向に着目して表やグラフに的確に表現し,それらを用いて問題解決したり,解決の過程や結果を多面的に捉え考察したりする力 | |
| 第5学年 | 数とその表現や計算の意味に着目し,目的に合った表現方法を用いて数の性質や計算の仕方などを考察する力 | 図形を構成する要素や図形間の関係などに着目し,図形の性質や図形の計量について考察する力 | 伴って変わる二つの数量やそれらの関係に着目し,変化や対応の特徴を見いだして,二つの数量の関係を表や式を用いて考察する力 | 目的に応じてデータを収集し,データの特徴や傾向に着目して表やグラフに的確に表現し,それらを用いて問題解決したり,解決の過程や結果を多面的に捉え考察したりする力 | |
| 第6学年 | 数とその表現や計算の意味に着目し,発展的に考察して問題を見いだすとともに,目的に応じて多様な表現方法を用いながら数の表し方や計算の仕方などを考察する力 | 図形を構成する要素や図形間の関係などに着目し,図形の性質や図形の計量について考察する力 | 伴って変わる二つの数量やそれらの関係に着目し,変化や対応の特徴を見いだして,二つの数量の関係を表や式,グラフを用いて考察する力 | 身の回りの事象から設定した問題について,目的に応じてデータを収集し,データの特徴や傾向に着目して適切な手法を選択して分析を行い,それらを用いて問題解決したり,解決の過程や結果を批判的に考察したりする力 | |
| 中 | A 数と式 | B 図 形 | C 関 数 | D データの活用 | |
| 第1学年 | 数の範囲を拡張し,数の性質や計算について考察したり,文字を用いて数量の関係や法則などを考察したりする力 | 図形の構成要素や構成の仕方に着目し,図形の性質や関係を直観的に捉え論理的に考察する力 | 数量の変化や対応に着目して関数関係を見いだし,その特徴を表,式,グラフなどで考察する力 | データの分布に着目し,その傾向を読み取り批判的に考察して判断したり,不確定な事象の起こりやすさについて考察したりする力 | |
| 第2学年 | 文字を用いて数量の関係や法則などを考察する力 | 数学的な推論の過程に着目し,図形の性質や関係を論理的に考察し表現する力 | 関数関係に着目し,その特徴を表,式,グラフを相互に関連付けて考察する力 | 複数の集団のデータの分布に着目し,その傾向を比較して読み取り批判的に考察して判断したり,不確定な事象の起こりやすさについて考察したりする力 | |
| 第3学年 | 数の範囲に着目し,数の性質や計算について考察したり,文字を用いて数量の関係や法則などを考察したりする力 | 図形の構成要素の関係に着目し,図形の性質や計量について論理的に考察し表現する力 | 関数関係に着目し,その特徴を表,式,グラフを相互に関連付けて考察する力 | 標本と母集団の関係に着目し,母集団の傾向を推定し判断したり,調査の方法や結果を批判的に考察したりする力 |
数学的な見方・考え方とは各領域では具体的にどのように捉えたり考えたりすることなのかについては,「数学的な見方・考え方と算数科領域のねらい」をご覧ください。
※ 出典:文部科学省「小学校学習指導要領解説算数編 第1章総説 2算数科改訂の趣旨及び要点(3)算数科の内容構成の改善 資質・能力(「思考力,判断力,表現力等」「学びに向かう力,人間性等」)(図3)」平成29年6月[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2017/07/25/1387017_4_1_1.pdf(参照2018/04/12)
4 「数学的な見方・考え方」を考える
(1)二段階の算数科の数学的な見方
数学的な見方は,小学校では,発達段階を考慮して二段階で構成されます。
例えば,量と測定であれば,
①「量(ものの大きさ)に着目する」→②「ものの大きさのもとになる大きさ(単位)に着目する」
図形であれば,
①「形に着目する」→②「図形の構成要素に着目する。それらの位置関係に着目する。形や大きさなどの観点から図形相互の関係に着目するなど」
となっています。
数学的な見方の前段①「形に着目する」は,対象には様々な属性がありますが,まずは形に目を向けることです。ものの形を認めたり,形の特徴を捉えたりすることです。そのこと自体が抽象化していることになりますが,①の見方は,数学的な厳密さを求めていません。
数学的な見方の後段②「図形の構成要素やその位置関係に着目する」は,単位の考えとして数学的な考え方に含まれるものです。
①は,日常の事象を算数の舞台に載せるときに,②は算数の事象を算数の問題にするときに,中心的に働く見方と考えられます。また,①は対象の様々な属性の中から数量や図形そのものに着目する見方,②は,抽象化された数量や図形,または,それらの関係に着目して捉える見方とも言えます。
例えば,
・ 第1学年では,ものの形を認めたり,形の特徴を捉えたりします。
これは,①「形に着目する」数学的な見方です。
・ 第2学年では,図形を構成する要素に着目して,三角形や四角形などを,
・ 第3学年では,二等辺三角形や正三角形などの図形について理解できるようにします。
これらは,②「図形の構成要素に着目する」数学的な見方です。
・ 第4学年では,図形の構成要素及びそれらの位置関係に着目して,平行四辺形やひし形などの平面図形及び直方体などの立体図形について理解できるようにします。
これは,さらに「位置関係」の見方が加わり,②「構成要素及びそれらの位置関係に着目する」数学的な見方です。
このように算数科の場合は,数学的な見方には,子どもの見方の育ちや考察対象に合わせて以下があると考えられます。
ア 事象を,様々な属性から数量や図形そのものを認め捉えること
イ 事象を,数量や図形についての概念等に着目してその特徴や本質を捉えること
ウ 事象を,数量や図形の関係についての概念等に着目してその特徴や本質を捉えること
イとウは,考察対象の違いです。
ウの例として,直線や平面の位置関係に着目して,平行や垂直の関係について考察します。これは,2直線の関係という算数の世界の事象を,どんな2直線の関係があり得るかを考える算数の問題をつくる場面です。「関係」を捉えることは,より高次な数学的な見方です。
(2)問題解決の過程で発揮
平成29年改訂学習指導要領では,数学的活動における問題発見・解決の過程を主に二つの過程で示しています。
一つは,「日常生活や社会の事象の数学化」です。日常生活や社会の事象を数理的に捉え,数学的に表現・処理し,問題を解決し,解決過程を振り返り得られた結果の意味を考察する過程です。
もう一つは,「数学の事象の数学化」です。数学の事象から問題を見いだし,数学的な推論などによって問題を解決し,解決の過程や結果を振り返って統合的・発展的に考察する過程です。
学習過程では,これらの過程を意識し,生徒が目的意識をもって遂行できるようにします。また,各場面で言語活動を充実し,それぞれの過程や結果を振り返り,評価・改善できるようにすることも大切とされます。
「日常生活や社会の事象の数学化」では,現実世界の事象を考察する際に,目的に応じて必要な観点をもち,その観点から事象を理想化したり抽象化したりして,事象を数量や図形及びそれらの関係などに着目して数学の舞台にのせて考察します。
数学的な見方・考え方を働かせ,事象を目的に応じて数学の舞台にのせたものが「数学的に表現した問題」です。
そして,数学的に表現した問題をより特定なものに焦点化して表現・処理し,得られた結果を解釈したり,類似の事象にも活用したりして適用範囲を拡げます。
「数学の事象の数学化」では,数学的な見方・考え方を働かせ,数量や図形及びそれらの関係などに着目し,観察や操作,実験などの活動を通して,一般的に成り立ちそうな事柄を予想します。
この予想した事柄に関する問いが「数学的に表現した問題」です。
そして,数学的に表現した問題をより特定なものに焦点化して表現・処理したり,得られた結果を振り返り統合的・発展的に考察したりします。
このように,数学的な見方・考え方は問題発見・解決の過程で中心的な働きをします。それらの資質・能力を必要なとき働かせ,発揮できるようにすることが大切です。
資料
「見方・考え方」の意義
(1)各教科等の特質に応じた「見方・考え方」[2]
○ 子供たちは,各教科等における習得・活用・探究という学びの過程の中で,各教科等で習得した概念(知識)や考え方を活用しながら,問いを見いだして解決したり,自分の考えを形成し表したり,思いを基に意味や価値を創造したりすることに向かう。
○ こうした学びの過程の中で,“どのような視点で物事を捉え,どのように思考していくのか”という,物事を捉える視点や考え方も鍛えられていく。例えば算数・数学科においては,事象を数量や図形及びそれらの関係などに着目して捉え,論理的,統合的・発展的に考えること,国語科においては,対象と言葉,言葉と言葉の関係を,言葉の意味,働き,使い方等に着目して捉え,その関係性を問い直して意味付けることなどである。
○ こうした「見方・考え方」は,各教科等の学習の中で活用されるだけではなく,大人になって生活していくに当たっても重要な働きをするものとなる。私たちが社会生活の中で,データを見ながら考えたり,アイディアを言葉で表現したりする時には,学校教育を通じて身に付けた「数学的な見方・考え方」や,「言葉による見方・考え方」が活用されている。いわば,頭の中にある「見方・考え方」を活用しながら,世の中の様々な物事を理解し思考し,よりよい社会や自らの人生を創り出していると考えられる。
○ この「見方・考え方」を支えているのは,各教科等の学習において習得した概念(知識)や考え方である。知識が豊かになれば見方も確かなものになり,思考力や人間性が深まれば考え方も豊かになる。いわば,資質・能力が,学習や生活の場面で道具として活用されているのが「見方・考え方」であり,資質・能力を,具体的な課題について考えたり探究したりする際に必要な手段として捉えたものであると言えよう。
○ 各教科等を学ぶ本質的な意義の中核をなすのが「見方・考え方」であり,教科等の教育と社会をつなぐものである。子供たちが学習や人生において「見方・考え方」を自在に働かせられるようにすることにこそ,教員の専門性が発揮されることが求められる。
○ こうした「見方・考え方」は,学習指導要領において長年用いられてきている用語であるが,その内容については必ずしも具体的に説明されてはこなかった。今回の改訂においては,これまで述べたような観点から「見方・考え方」を改めて明らかにし,それを軸とした授業改善の取組を活性化しようとするものである。
○ 次期学習指導要領等が目指すのは,学習の内容と方法の両方を重視し,子供たちの学びの過程を質的に高めていくことである。単元や題材のまとまりの中で,子供たちが「何ができるようになるか」を明確にしながら,「何を学ぶか」という学習内容と,「どのように学ぶか」という学びの過程を組み立てていくことが重要になる。「見方・考え方」を軸としながら,幅広い授業改善の工夫が展開されていくことを期待するものである。
(2)算数科・数学科における「見方・考え方」[3]
○ 算数科・数学科の学習においては,「数学的な見方・考え方」を働かせながら,知識・技能を習得したり,習得した知識・技能を活用して探究したりすることにより,生きて働く知識となり,技能の習熟・熟達にもつながるとともに,より広い領域や複雑な事象を基に思考・判断・表現できる力が育成される。このような学習を通じて,「数学的な見方・考え方」が更に成長していくと考えられる。
○ また,算数科・数学科において育成を目指す「学びに向かう力・人間性等」についても,「数学的な見方・考え方」を通して社会や世界にどのようにかかわっていくかが大きく作用しており,「数学的な見方・考え方」は資質・能力の三つの柱である「知識・技能」,「思考力・判断力・表現力等」,「学びに向かう力・人間性等」の全てに働くものであり,かつ全てを通して育成されるものとして捉えられる。
○ 「数学的な見方・考え方」のうち,「数学的な見方」については,事象を数量や図形及びそれらの関係についての概念等に着目してその特徴や本質を捉えることであると整理することができる。
○ また,「数学的な見方・考え方」のうち,「数学的な考え方」については,目的に応じて数・式,図,表,グラフ等を活用し,論理的に考え,問題解決の過程を振り返るなどして既習の知識・技能等を関連付けながら統合的・発展的に考えることであると整理することができる。
○ これらを踏まえると,算数科・数学科において育成される「数学的な見方・考え方」については,「事象を数量や図形及びそれらの関係などに着目して捉え,論理的,統合的・発展的に考えること」として再整理することが適当である。
[2]文部科学省中央教育審議会初等中等教育分科会教育課程部会「次期学習指導要領等に向けたこれまでの審議のまとめ」(第1部)p33,34平成28年8月26日[ONLINE]http://www.mext.go.jp/component/b_menu/shingi/toushin/__icsFiles/afieldfile/2016/09/09/1377021_1_1_11_1.pdf(参照2017/05/14)
[3]文部科学省中央教育審議会初等中等教育分科会教育課程部会「次期学習指導要領等に向けたこれまでの審議のまとめ」(第2部)(算数,数学,理科,高等学校の数学・理科にわたる探究科目,生活,音楽,芸術(音楽))p156,157平成28年8月26日[ONLINE]http://www.mext.go.jp/component/b_menu/shingi/toushin/__icsFiles/afieldfile/2016/09/09/1377021_1_4.pdf(参照2017/05/14)
学校段階ごとの領域別数学的な見方・考え方
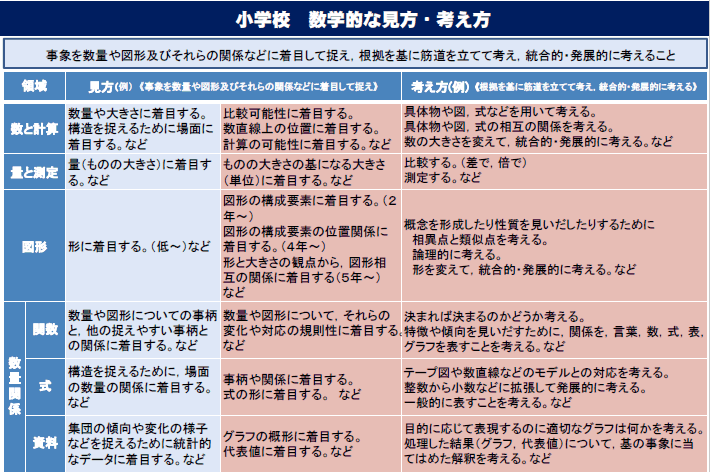 ※ 出典 文部科学省 教育課程部会算数・数学ワーキンググループ(第8回)配付資料参考資料2P5「数学的な見方・考え方」平成28年5月24日再掲[ONLINE]http://www.mext.go.jp/b_menu/shingi/chukyo/chukyo3/073/siryo/__icsFiles/afieldfile/2016/06/21/1372244_12.pdf(参照2017/05/14)
※ 出典 文部科学省 教育課程部会算数・数学ワーキンググループ(第8回)配付資料参考資料2P5「数学的な見方・考え方」平成28年5月24日再掲[ONLINE]http://www.mext.go.jp/b_menu/shingi/chukyo/chukyo3/073/siryo/__icsFiles/afieldfile/2016/06/21/1372244_12.pdf(参照2017/05/14)
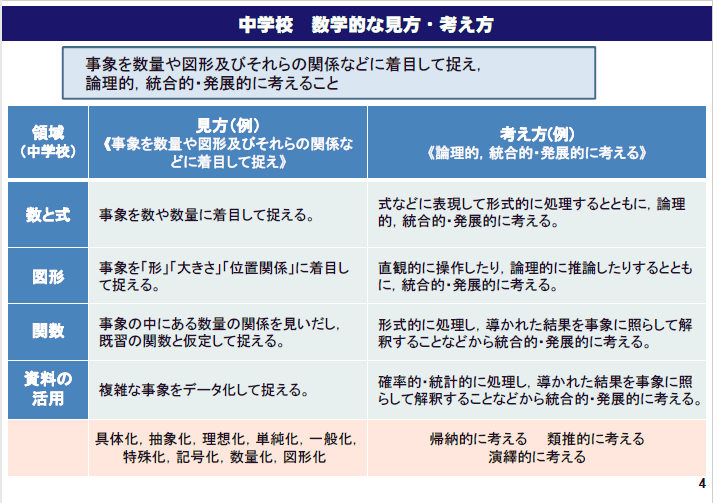 ※ 出典 文部科学省 教育課程部会算数・数学ワーキンググループ(第8回)配付資料参考資料2P4「数学的な見方・考え方」平成28年5月24日[ONLINE]http://www.mext.go.jp/b_menu/shingi/chukyo/chukyo3/073/siryo/__icsFiles/afieldfile/2016/06/21/1372244_12.pdf(参照2017/05/14)
※ 出典 文部科学省 教育課程部会算数・数学ワーキンググループ(第8回)配付資料参考資料2P4「数学的な見方・考え方」平成28年5月24日[ONLINE]http://www.mext.go.jp/b_menu/shingi/chukyo/chukyo3/073/siryo/__icsFiles/afieldfile/2016/06/21/1372244_12.pdf(参照2017/05/14)
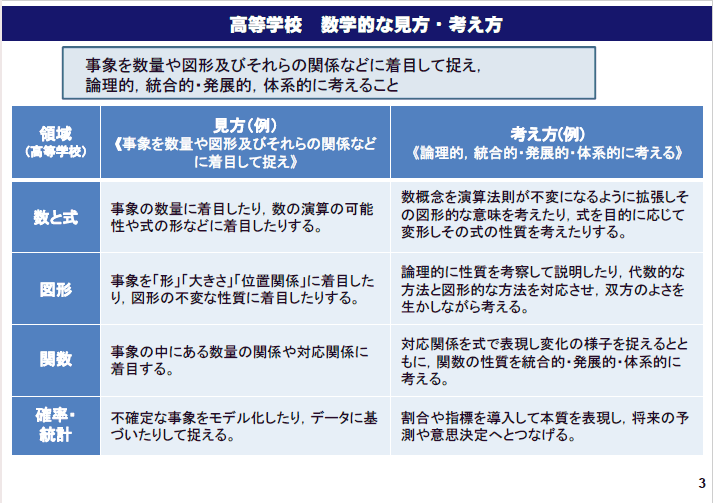 ※ 出典 文部科学省 教育課程部会算数・数学ワーキンググループ(第8回)配付資料参考資料2P3「数学的な見方・考え方」平成28年5月24日[ONLINE]http://www.mext.go.jp/b_menu/shingi/chukyo/chukyo3/073/siryo/__icsFiles/afieldfile/2016/06/21/1372244_12.pdf(参照2017/05/14)
※ 出典 文部科学省 教育課程部会算数・数学ワーキンググループ(第8回)配付資料参考資料2P3「数学的な見方・考え方」平成28年5月24日[ONLINE]http://www.mext.go.jp/b_menu/shingi/chukyo/chukyo3/073/siryo/__icsFiles/afieldfile/2016/06/21/1372244_12.pdf(参照2017/05/14)
【まとめ】
1 数学的な見方・考え方とは,「事象を,数量や図形及びそれらの関係などに着目して捉え,(論理的,)統合的・発展的に考えること」
・ 数学的な見方:事象を数量や図形及びそれらの関係についての概念等に着目してその特徴や本質を捉えること
・ 数学的な考え方:目的に応じて図,数,式,(数,式,図,)表,グラフ等を活用しつつ,根拠を基に筋道を立てて考え(論理的に考え),問題解決の過程を振り返るなどして既習の知識及び技能を関連付けながら,統合的・発展的に考えること
※青字小学校,( )中学校
2 小学校算数科の数学的な見方については,次のように整理できる。
・ 子どもの見方の育ちのレベルや考察対象に合わせて厳密さを求めない数学的な見方
・ 数量や図形そのものに着目して日常の事象を算数の舞台に載せるという数学的な見方
・ 数量や図形の関係に着目して算数の事象を算数の問題に数学化する数学的な見方
3 日常生活や社会の事象の数学化,数学の事象の数学化により数学的に表現した問題を解決し,過程を振り返り得られた結果の意味を考察したり,過程や結果を振り返って統合的・発展的に考察したりする過程で,数学的な見方・考え方が発揮される。
4「見方」と「考え方」は車の両輪であり,「深い学び」を実現するには見方・考え方の育成が欠かせない。