相関図（散布図）の意味とエクセルを使った作り方

相関図（散布図）や相関表はどのように作るのでしょうか。また，作成上の留意点は何でしょうか。

平面上に互いに直交する２直線ＯＸ,ＯＹを設け，その各々の上に適当に目盛りを付しほどこし，得られた資料の値の組(x_i,y_i)(i=1,2,…,n)を座標とする点をうって作ったものを変量ＸとＹの相関図と言います。

【相関図の作り方】
1.　検討したい２つの量的変数を特定する
2.　平面上に互いに直交する２直線ＯＸ,ＯＹを設け，その各々の上に適当に目盛りを付す
3.　独立変数をＸ軸，従属変数をＹ軸にする
4.　点をうつ
5.　外れ値は採用を検討し，異常値は修正する
【作成上の留意点】
・　相関図の「相関がある」という結果を切り口として，要因や事実を探ることが大切です。相関図の２つの変数は独立です。因果関係だとは言えないことに注意が必要です。
・　ｘとｙの取り得る値がデータ数に比べて少なく，重なる点が多くなる場合は，相関表を作成します。
・　実際の相関図の作成にあたっては，Microsoft Excel の利用がおすすめです。

１　相関図（散布図）の活用例

（１）旅行先別 価格満足度比較

次の相関図（散布図）をご覧ください。※デスティネーション：旅行目的地，旅行先

各デスティネーションに対する価格満足度評価結果を，旅行構成要素別に散布図で示すと下図のようになっていた。 各デスティネーション間において，ホテルの価格満足度とレストランの価格満足度とに緩やかな相関性が見られた。現地交通機関とショッピングの間も同様であった。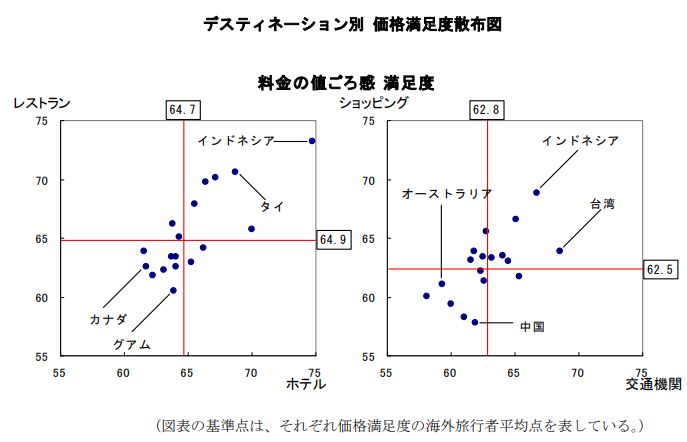

国土交通省総合政策局「海外旅行者満足度・意識調査報告書（平成20年7月）デスティネーション別 価格満足度散布図」[ONLINE]http://www.mlit.go.jp/common/000019459.pdf(2018.11.2参照)

国土交通省総合政策局では，海外旅行者数の拡大を図るため，「海外旅行者満足度・意識調査」を通して，若年層を中心とした日本人の海外旅行離れの原因究明を行いました。
内容としては，海外旅行に対する日本人の意識・心理や，旅行者の満足度等についての調査・分析です。

上図は，国土交通省総合政策局が，旅行先別に「観光」「食」「宿」「ショッピング」等の旅行構成要素別に，料金の値ごろ感，満足度を散布図に表したものです。
左図は，
「良い施設やサービスのホテルを安く利用できる満足度」と「美味しくてサービスの良いレストランを安く利用できる満足度」とに，相関があることを示しています。
言い換えると「ホテルが価格からみて満足なほど，レストランも価格からみて満足」となるでしょう。
右図は，
「良いサービスの交通機関を安く利用できる満足度」と「良い商品やサービスのショッピングを安く利用できる満足度」とに，相関があることを示しています。
「交通機関や手段が価格からみて満足なほど，ショッピングも価格からみて満足」となるでしょう。

「ホテル」と「レストラン」，「交通機関」と「ショッピング」は，一方が高いほど他方も高い傾向にある「正の相関」という相関関係です。

「正の相関」等の相関図の読み方は別稿で詳しく述べます。

相関図の相関関係を言葉，数，図形で表現する方法

（２）交通機関の価格満足度とショッピングの価格満足度とに相関

交通機関の価格満足度の調査では，現地の交通手段について，
・　空港や駅などの施設の充実度，快適性
・　時間の正確さやダイヤの利便性などの運行
・　乗り物の快適性
・　乗務員や係員の接客態度や専門性
・　案内表示やアナウンス
が，料金に照らして値ごろ感があるかを調べています。

ショッピングの価格満足度の調査では，ショッピングについて，
・　お店の外観，店内の雰囲気
・　店員の接客態度や商品知識
・　品揃えの豊富さ
・　商品のデザイン，品質等
が，料金に照らして値ごろ感があるかを調べています。

一般に，このような複数の調査項目について，それぞれの相関を調べ，特徴的な相関があれば要因や背景を分析します。
先の調査結果から，このような「交通機関の価格満足度とショッピングの価格満足度とに緩やかな相関性」がみられました。

この結果は，単に相関があるということだけですが，筆者には興味深いものです。

あるＡ地という旅行先を訪問するとします。
まずは，交通手段を利用して目的地に移動します。
Ａ地の空港や駅は施設が充実，ダイヤは正確です。乗り物も快適です。しかも料金が安い。
このようなＡ地にある商店でショッピングすれば，安くて質の良い商品が買える可能性が高いと考えられます。

一方，Ｂ地を訪問するとします。
Ｂ地の交通機関は不便です。目的地にたどり着くのは容易ではありません。ダイヤも大幅な遅延があります。遅延に対するアナウンスや他の交通手段の案内もありません。しかも運賃は高めです。
このようなＢ地にある商店でショッピングすれば，Ａ地と同様に，安くて質の良い商品が買える可能性が高いでしょうか。おそらく可能性は低いと考えられます。

このことは，筆者の推測であり，調査結果からは言えることではありません。しかしながら，可能性を感じます。
「相関がある」ということは，単なる結果であって，そのことを切り口として，要因や事実を探ることが大切です。

先の「交通機関」と「ショッピング」とに相関がみられる例では，その要因として，訪問先の政策や経済力，国民性などが背景にあり，それが交通機関とショッピングに象徴的に現れていると考えられます。

（３）その他の例

①　清涼飲料水摂取と齲歯数の相関

論文中では，「調査対象として用いた3歳児の一人平均齲歯数（うし，虫歯）を縦軸とし,清涼飲料の住民一人平均年間消費本数を横軸として,齲歯数の多い管内と少ない管内を表現したもの」として相関図を利用しています。
それによると，「清涼飲料水の摂取」と「齲歯数」とに正の相関がみられます。
このデータなどから，清涼飲料摂取によって齲歯多発傾向が強くみられることなどを論じています。

栗田 啓子「幼児の齲歯の多発と生活習慣との相関関係についての研究　偏相関係数を用いた統計的分析による」J-STAGEトップ/口腔衛生学会雑誌/1983年32巻5号p.541-562[ONLINE]https://www.jstage.jst.go.jp/article/jdh1952/32/5/32_5_541/_article/-char/ja/(2018.11.7)

②　アミノ酸含有量と煎茶価格の相関

下記は，煎茶の価格と全窒素量及び遊離アミノ酸の組成や含量との関係を検討した結果を報告した論文の一資料です。
「17種類のアミノ酸の中で価格と間に最も高い関係があったのは,図4に示した相関係数が0.91のアルギニンであった」と論じています。

次の相関図と相関係数によれば，「アルギニンの含有量」と「煎茶の価格」には，強い正の相関がみられます。

向井 俊博, 堀江 秀樹, 後藤 哲久「煎茶の遊離アミノ酸と全窒素の含量と価格との関係について」J-STAGEトップ/茶業研究報告/1992年1992巻76号p.45-50
[ONLINE]https://www.jstage.jst.go.jp/article/cha1953/1992/76/1992_76_45/_article/-char/ja/(2018.11.7)

相関の強さを表す相関係数の定義と求め方








２　相関図の意味と作り方

（１）相関図とは

「海外旅行者満足度・意識調査報告書」で散布図と表記された図は，相関図とも言います。

相関図を作成すると，点の散らばり具合から，２つの変量Ｘ，Ｙの相関関係の特徴を視覚的・直感的に捉えることができます。
なお，本稿では，「変量」と下記に述べる「量的変数」は同義として表記します。

（２）相関図の作り方

①　２つの量的変数を特定する

まず，検討したい２つの量的変数を特定します。大きさや多さなど量的に変化する特性をもつ２つの量です。

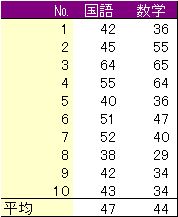
例えば，国語科と数学科のそれぞれのペーパーテストによる得点を調査の対象とします。調査結果からそれらの相関関係を捉えることとします。

国語科の得点　と　数学科の得点　との　相関関係

このとき，測定の妥当性と信頼性を吟味することが大切です。ペーパーテストの得点は測れますが，その結果だけから「学力」について断定することはできません。測りたいものが的確に捉えられているか，測定結果が一貫しているか，十分検討することが大切です。

②　データを集め，表に集計する

必要な試験を実施し，データを集めます。結果は次の表のようでした。

③　平面に直交する座標軸を作る

次に，一方の量的変数をＸ，他方をＹとして，平面上に互いに直交する２直線ＯＸ,ＯＹを設け，その各々の上に設定した単位に基づいて適当に目盛ります。

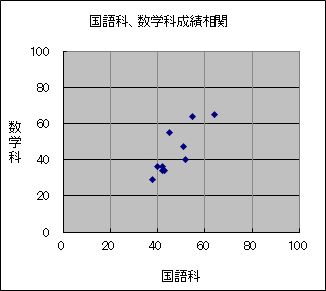
④　該当する座標に点をとる

そして，Ｘ軸とＹ軸を垂直に交わらせた平面上に各対象をプロットします。
(42,36)のように，国語科得点と数学科得点の組の点をプロットしていきます。

（３）エクセルを使った相関図（散布図）の作り方

①　エクセルの利用を推奨

実際の相関図の作成にあたっては，Microsoft Excel の利用をお勧めします。
シートに一旦データを入力すれば，多様なデータ分析が容易にできるようになります。

ＰＣに，アプリケーションの Excel をインストールしていなくても，Microsoft アカウントをもっていれば Web 上で動作する Excel Online を無料で利用できます。
ウインドウズのみならずマックでも，利用できます。
Excel Onlineは，Microsoftが提供するクラウド版 Excel です。Excelに比べると機能は制限されますが，Excelデータをクラウド上で無料で作成・保存・編集・共有できます。Excelデータは，Microsoft OneDrive に保存します。もちろんＰＣにもダウンロードできます。

詳細な説明は，Microsoft OneDrive などの情報をご確認ください。サインインはこちらです。
Office.com[ONLINE]https://www.office.com/signin
アカウントがない場合でも作成できます。

②　相関図の作成手順

さて，Excelを使って相関図を作成するには，次の手順によります。Excel ヘルプでは，相関図を散布図として説明しています。
なお，下記の図による説明は Microsoft Excel 2013 ですが，Office 365 でもほぼ同様です。

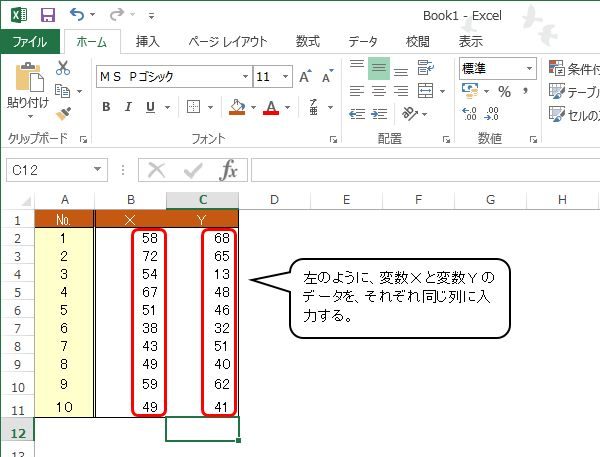
ア　データ一覧の作成

次のように，相関図（散布図）のもとになるデータの一覧を作成します。変数ＸのデータはＢ列，変数ＹのデータはＣ列に縦に入力します。

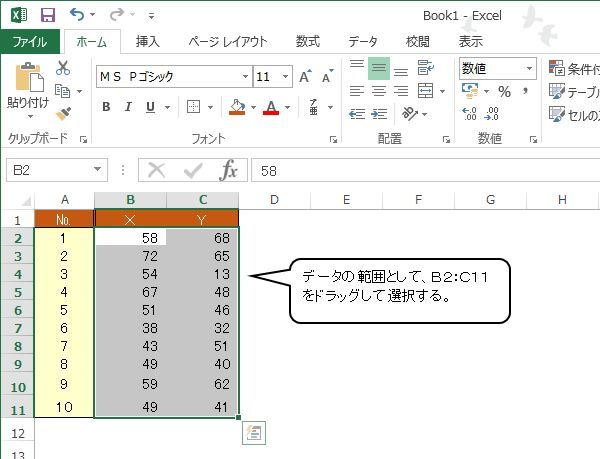
イ　データ範囲の選択

相関図（散布図）を作成するため，元データの範囲を選択します。
セルＢ２からセルＣ１１を選択します。列データ（Ｂ列とＣ列）のみを指定します。
一般のグラフ作成では，項目名やNo.なども含めて選択します。しかし，相関図では，データ列のみを選択することに注意します。

ウ　散布図の表示

「挿入」→「グラフ」→「散布図」を選択します。散布図の種類の選択は，点のみで表示される左上の図を選択します。
すると，自動で相関図（散布図）が作成されます。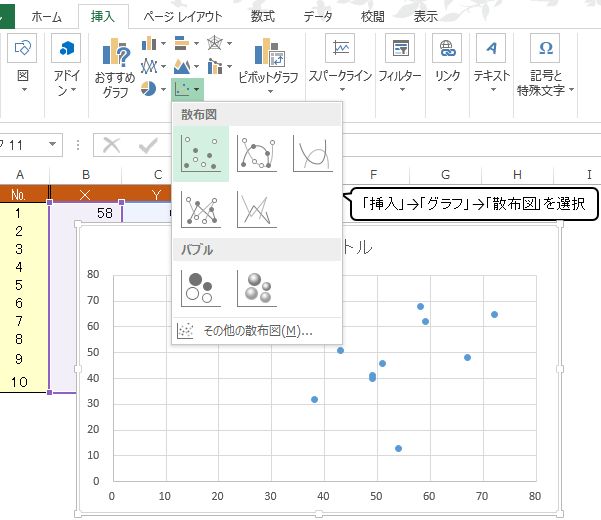

エ　詳細設定

目盛りやタイトルなどの詳細な設定は，「+」をクリックしてダイアログを開いて設定します。
軸，軸ラベル，グラフタイトル，データラベル，誤差範囲，目盛線，凡例，近似曲線が設定できます。

Office 365 では同様の操作ですが，Excel Online では「グラフ」メニューのリボンからタイトルや軸ラベルなどを選択するなど操作方法が異なります。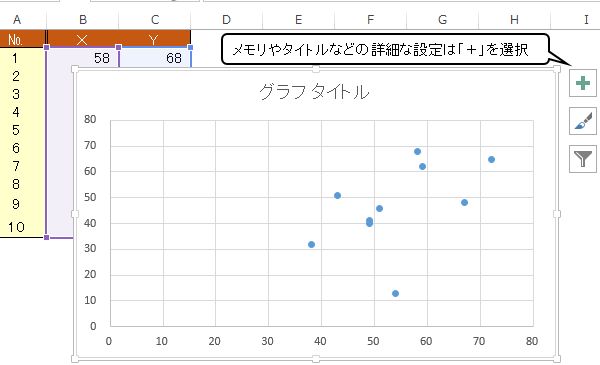

（４）作成上の留意点

①　座標軸の決め方

このとき，伴って変わる変数をＹ軸にします。

独立変数をＸ軸，従属変数をＹ軸にします。（回帰分析をするとき，Ｘ軸（横軸）の独立変数は予測変数，説明変数。Ｙ軸（縦軸）の従属変数は基準変数，目的変数，被説明変数ということもあります）
因果関係で言えば，原因側をＸ軸，結果側をＹ軸にします。これは，作成者が読み手や聞き手に説明をしやすくするためです。

本来，相関図における２つの量的変数は，それぞれ独立しています。対等です。ですから，どちらをＸ軸，あるいはＹ軸にしてもかまいません。
しかし，その後の論理をどのように展開して説明するかで，説明しやすいＸ軸，Ｙ軸の決め方があります。
例えば，
「国語の力が，数学の学力にも影響する」と説明したい場合は，国語科の得点をＸ軸，数学科の得点をＹ軸にします。
また，「数学科の論理的思考力が，国語科の思考力に影響する」と説明したい場合は，算数科の得点をＸ軸，国語科の得点をＹ軸にします。
そのように相関図を作成する方が，作成者ばかりでなく読み手も理解しやすくなります。

あくまでも，相関図の２つの変数は独立しています。
一方が原因で他方が結果という因果関係であるとは言えません。相関関係があると言えるだけです。説明の際には，相関図の結果分析の説明と要因の推測の説明を，読み手が分かるように区別して表記します。

②　外れ値，異常値への対応

作成した相関図に，点の散らばり具合を見ると飛び離れた点がある場合があります。

ア　外れ値は検討

飛び離れた点は，外れ値である場合があります。
統計上，他の値から大きく外れた値です。何か特殊な状況下で生まれた値，特殊なデータの可能性があります。外れ値を含めて分析するかどうかは検討が必要です。代表値として不都合な場合は外れ値を除外することがありますが，外れ値が問題解決のきっかけとなる重要なデータであることがあるからです。

イ　異常値は修正

また，飛び離れたその点は，測定ミス・記録ミス等による異常値である可能性があります。
ミスによる異常値の場合は，再確認して修正入力が必要です。








【まとめ】
・　平面上に互いに直交する２直線ＯＸ,ＯＹを設け，その各々の上に適当に目盛りをほどこし，得られた資料の値の組(x_i,y_i)(i=1,2,…,n)を座標とする点をうって作ったものを変量ＸとＹの相関図という
・　相関図の２つの変数は独立であり，一方が原因で他方が結果という因果関係とは言えない
・　「相関がある」という結果を切り口として，要因や事実を探ることが大切である

相関図の作り方
1.　 妥当性と信頼性に留意して，検討したい２つの量的変数を特定する
2.　平面上に互いに直交する２直線ＯＸ,ＯＹを設け，その各々の上に適当に目盛りを付す
3.　説明したい独立変数をＸ軸，従属変数をＹ軸にする
4.　点をうつ
5.　外れ値は採用を検討し，異常値は修正する