- コピー用紙を使って正三角形を作るには,どのようにするとよいのでしょう。
- 同一番号のA判の短辺と長辺,B判の短辺と長辺の比は,\(1:\sqrt{2}:\sqrt{\dfrac{3}{2}}:\sqrt{3}\)。A判単体の短辺:長辺:対角線\(=1:\sqrt{2}:\sqrt{3}\) です。これらと正三角形の性質を使って,A判等に正三角形を作ります。以下,4つの作り方を紹介します。
1 短辺で二つ折りにして,折り目上に短辺の一つの端点から短辺と等しい長さを移して頂点を決め方法
2 同サイズ同番号のA判二枚とB判二枚を各短辺と長辺を一頂点に揃え並べて正三角形の頂点を確定する方法
3 \(\dfrac{\sqrt{3}}{2}\)の垂線を移す道具を作って頂点を確定する方法
4 \(\dfrac{\sqrt{3}}{2}\)を長辺に移して短辺の垂直二等分線との交点を求める方法
1 A判B判と正三角形
本稿では,A判とB判の紙を使った正三角形の作り方を考えます。
A判の短辺を 1 とした辺の比を利用するなど,特徴ある辺の比を利用して,正三角形を4つの方法で作ります。
そのために,まずA判とB判の規格,そして,正三角形の定義と性質を確かめましょう。
(1)A判B判の辺の比
コピー用紙などの紙のサイズには規格があり,A判とB判では次のように辺の比が決まっています。
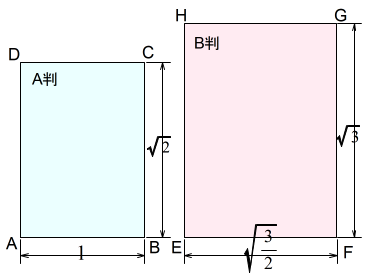 A判の短辺\(a_x\)を 1 とすると,同一番号のA判の短辺\(a_x\)と長辺\(a_y\),B判の短辺\(b_x\)と長辺\(b_y\)の比は,次のようになります。
A判の短辺\(a_x\)を 1 とすると,同一番号のA判の短辺\(a_x\)と長辺\(a_y\),B判の短辺\(b_x\)と長辺\(b_y\)の比は,次のようになります。
$$a_x:a_y:b_x:b_y=1:\sqrt{2}:\sqrt{\dfrac{3}{2}}:\sqrt{3}$$
これらをそれぞれ2等分したA判B判においても,同様の比率になります。例えば,A4判とB4判の辺の比とA5判とB5判の辺の比は上記と同じです。
この比率等の詳細については,別稿「A判とB判の図形としての無理数の関係」で触れているので参照ください。
(2)正三角形の定義と性質
まず,正三角形の定義と性質を振り返ってみましょう。
正三角形の定義は,小学校算数教科書では「3つの辺の長さが,みんな同じ三角形」*1,中学校数学教科書では「3つの辺がすべて等しい三角形」*2としています。
数学事典では,「3つの辺の長さが等しく,3つの頂点の内角が等しい三角形」*3と説明しています。ただし,これは,多角形の解説項目の一つとして「定理」として説明しています。
その説明の前段で,三角形を次のように定義しています。「3個の点A B,Cが一本の直線上にないとする。このとき,3個の線分AB,BC,CAを定める。この3点と3線分の作る図形を三角形という。…以下略…」*3
正多角形「平面上の閉じた凸多角形で,その辺及び内角がそれぞれすべて合同であるものを正多角形(regular polygon)という。その頂点の個数(=辺の個数)が \(n\) であるとき,正\(n\)角形(正\(n\)辺形)という。」*4
「3つの頂点の内角が全て等しい三角形」を定義とすることもできます。どちらか一方を定義とすれば,他方は性質(定理)となります。
*1 啓林館「算数用語集」[ONLINE]https://www.shinko-keirin.co.jp/keirinkan/sansu/WebHelp/03/page3_15.html(cf.2020-07-05)
*2 啓林館数学2平成23年版
*3 新数学事典大阪書籍1979
*4 岩波数学辞典第二版
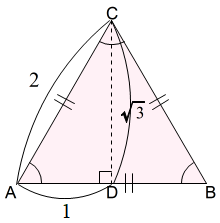 正三角形は,最も辺の数が少ない正多角形です。1つの内角は 60°,弧度法では \(\dfrac{π}{3}rad\) です。また一つの内角が 60°である二等辺三角形は正三角形となります。
正三角形は,最も辺の数が少ない正多角形です。1つの内角は 60°,弧度法では \(\dfrac{π}{3}rad\) です。また一つの内角が 60°である二等辺三角形は正三角形となります。
正三角形の一辺を垂直に2等分すると,垂直二等分線は対する頂点を通り,2つの合同な直角三角形に分割できます。このことは,一つの頂点から対辺に下ろした垂線と対辺の交点は,対辺の中点であるともいえます。このとき,垂線は頂点の内角の二等分線となっています。
正三角形を2分割した一つの直角三角形において,その辺の比は,三平方の定理より \(1:2:\sqrt{3}\) であり,角の大きさは,30°,60°,90°です。
正三角形は,線対称な図形です。その対称の軸は頂点から対辺に下ろした垂線です。対称の軸は3本あります。
本稿と直接関係はありませんが,正三角形は,内心(3内角の二等分線),外心(3辺の垂直二等分線),垂心(頂点から対辺に下ろした3垂線),重心(頂点と対辺の中点を結ぶ3線分)が全て一点に集まる唯一の三角形です。また,三角形の内心, 外心, 重心, 垂心のうち2つ以上が一致するとき,その三角形は正三角形であるといえます。
2 短辺と垂直二等分線
(1)見方・考え方
以下の方法は,A判とB判のどちらでも正三角形を作ることができます。
ここでは,A判の短辺 1 を基にする長さを使って正三角形を作ろうとしているため,A判を想定して考えることにします。
A判の短辺と長辺の比は,\(1:\sqrt{2}\) です。長辺 \(\sqrt{2}\) を一辺とする正三角形は,高さ \(\sqrt{2}\times
\dfrac{\sqrt{3}}{2}=1.224\dots\) も一辺 \(\sqrt{2}=1.414\dots\) も短辺 1 より長いので,紙に収まりません。一辺が 2 の正三角形はもとよりA判内に描けません。
そこで,内接する最大の正三角形ではありませんが,短辺 \(1\) を一辺とする正三角形を考えることとします。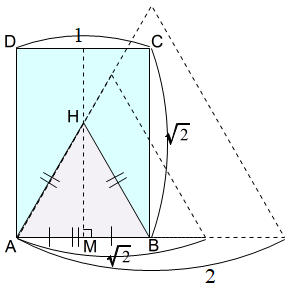 まず,□ABCD(以降,A判ABCDを□ABCDと記す)に正三角形ABHが描けたとします。
まず,□ABCD(以降,A判ABCDを□ABCDと記す)に正三角形ABHが描けたとします。
正三角形ABHは,ABを一辺とするので,3頂点のうち2頂点A,Bは決まります。残るは,3頂点目の頂点Hです。それが決まれば正三角形ABHを作れます。
頂点Hをとるには,\(AH=BH\) となる交点Hをとる,ABの垂直二等分線上に高さをとるなどが考えられます。
ここでは,\(AH=BH\) となる交点Hをとる方法を考えましょう。なぜなら,短辺 1 の長さを移すことは比較的容易だからです。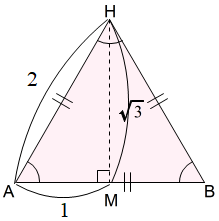 作図の鍵は,短辺 1 の長さを,頂点Hが交点となるように移すことです。
作図の鍵は,短辺 1 の長さを,頂点Hが交点となるように移すことです。
ところが,AHとBHの二辺を順に長さを移す方法は,紙を折る作業で正確に作るには手間がかかります。
そこで,二つ折りすれば簡単に折り目を付けられる垂直二等分線を利用します。頂点Hは対辺ABの垂直二等分線上にあります。点Aを中心として \(AB=AH\) となるよう長さを移して,垂直二等分線上に交点をとります。その交点が頂点Hです。
この方法によれば,\(\bigtriangleup AMH \equiv \bigtriangleup BMH\) なので,\(AB=AH=BH\) となり,三角形ABHは正三角形といえます。
したがって,以上の方法は,合同な直角三角形の性質を基に,長方形の短辺の長さと短辺の垂直二等分線を使った作り方といえます。
(2)作り方
① 二つ折りして開く
はじめに,長方形の短辺の垂直二等分線を作ります。
□ABCDにおいて,ABの中点をE,DCの中点をFとします。線分EFで折り,長辺ADと長辺BCを重ねます。そして,線分EFの折り目をつけて,元のように開きます。
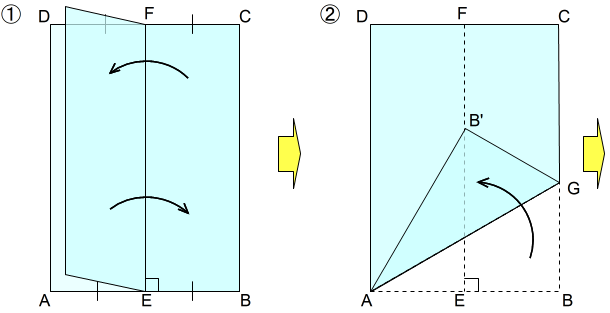
② 短辺の長さを二つ折りの折り目に移す
点Aを中心にABを半径としてEF上に交点をとります。EF上の交点を点B’とします。
実際には,頂点Aを押さえて\(AB=AB’\) となるように紙を引っ張りながらABを動かして(点Aを中心とした60°左回転),折り目EF上に点B’が乗る位置を見つけてAGで折ります。
③ 点B’の位置に印を入れる
折り目EF上の点B’の位置に,鉛筆などで印を入れます。その点B’が正三角形の頂点の一つです。
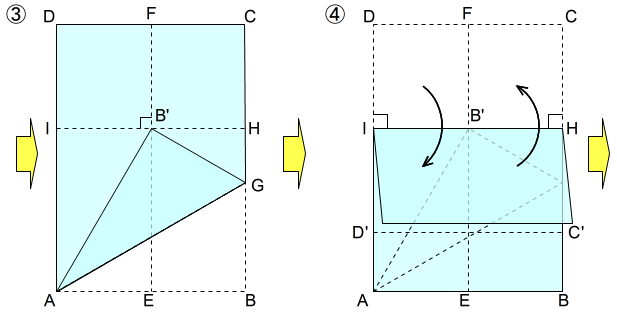
④ 点B’の位置に折り目を入れる
ADとID’,BCとHC’が重なることに注意して,折り目EFが重なるよう折って折り目を入れます。そして,元のように開きます。
これは必ずしも必要な操作ではありません。点B’の位置を明確にしたり,別の正三角形の作り方と比較するなど図形の分析に役立てたりする折り目です。
⑤ AB’,BB’の折り目を入れる
AB’,BB’の折り目を入れます。AB,AB’,BB’を三辺とする正三角形が,これで完成です。
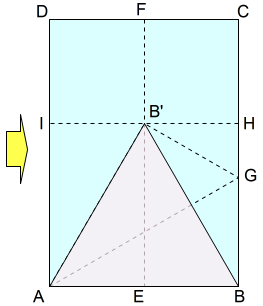
(3)解説
三角形ABB’は正三角形です。
その理由は,作図上 \(AB=AB’,AEB’\equiv BEB’\) となるよう作ったからです。
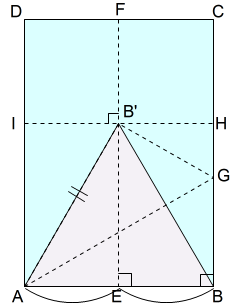
三角形AEB’と三角形BEB’において
□ABCDを二つ折りにしたことから,
\(AE=BE,\angle AEB’ = \angle BEB’ = \angle R,EB’\)共通 より,三角形AEB’と三角形BEB’は二辺挟角が等しいので,\(AEB’\equiv BEB’\)
したがって,\(AB’=BB’\)
もともと\(AB=AB’\) となるよう作図したので,
\(AB=AB’=BB’\) 三辺の長さが等しい三角形なので,三角形ABB’は正三角形といえます。
以上の正三角形を作る方法は,短辺で二つ折りにして,折り目上に短辺の一つの端点から短辺と等しい長さの点を取って作る方法です。これは,短辺と垂直二等分線を使った方法であり,正三角形を2等分する合同な直角三角形の性質を利用した作図方法です。
3 同番号A判短辺とB判長辺
(1)見方・考え方
正三角形の高さは,\(\sqrt{3}\) です。 \(\sqrt{3}\) といえば,A判の短辺に対するB判の長辺の長さです。この長さを高さとする正三角形を作ればよいことになります。
\(\sqrt{3}\) といえば,A判の短辺に対するB判の長辺の長さです。この長さを高さとする正三角形を作ればよいことになります。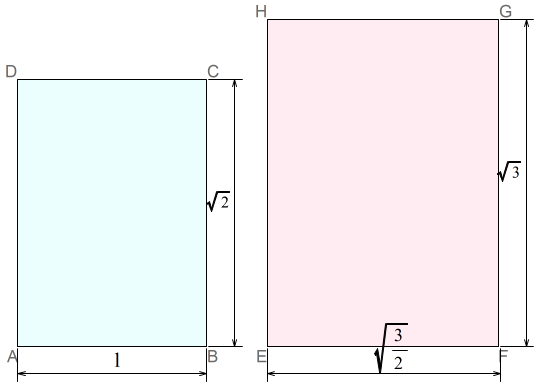 ところが,高さを\(\sqrt{3}\) とする正三角形をB判の中に描こうとすると,正三角形はB判からはみ出ます。なぜなら,B判の短辺は,\(EF=\sqrt{\dfrac{3}{2}}=1.2247\dots<2\)となり,2の長さの一辺が収まらないからです。
ところが,高さを\(\sqrt{3}\) とする正三角形をB判の中に描こうとすると,正三角形はB判からはみ出ます。なぜなら,B判の短辺は,\(EF=\sqrt{\dfrac{3}{2}}=1.2247\dots<2\)となり,2の長さの一辺が収まらないからです。
そこで,同サイズのB判を二枚用意し,B判の長辺そのものを高さとする正三角形を作ることを考えます。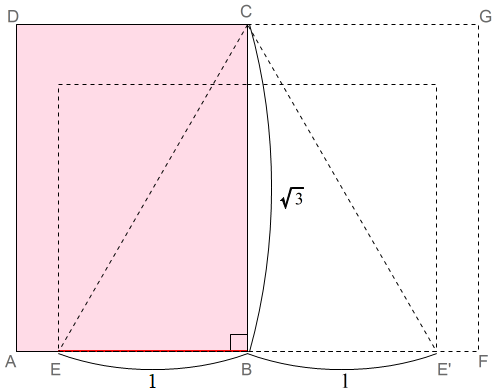
B判を二枚長辺を揃えて並べます。その上に正三角形が描けたとします。
すると,一つの頂点を点Cとする正三角形を描くには,頂点E,E’の確定が必要です。
そのためには,\(BE=BE’=1\) とするための 1 の長さが必要です。1 の長さは,A判の短辺です。
そこで,A判二枚を,図のように頂点Bを揃え,BCに長辺を揃えて配置すると,AB上に短辺の 1 の長さがとれます。これで,正三角形の頂点C,E,E’が確定できます。
(2)作り方
同サイズのA判とB判のそれぞれ二枚ずつで,正三角形を作ることができます。
まず,B判二枚を長辺BJを重ねて並べます。その上に,A判二枚を長辺BEをB判の長辺BJに重ねて並べます。それぞれの短辺は,頂点Bを揃えて,GH上に重ねます。
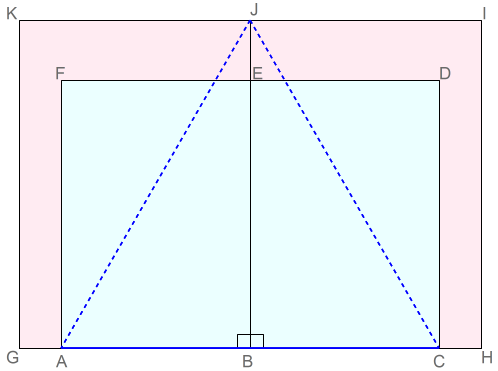 その時できるGH上の頂点Aと頂点Cが正三角形の頂点になります。これにより,頂点A,頂点C,頂点Jを結べば,\(AB=BC=1,BJ=\sqrt{3}\) となる正三角形ACJが作れます。
その時できるGH上の頂点Aと頂点Cが正三角形の頂点になります。これにより,頂点A,頂点C,頂点Jを結べば,\(AB=BC=1,BJ=\sqrt{3}\) となる正三角形ACJが作れます。
揃える手間はありますが,置くだけでできるの簡単に作れます。
別の方法として,A判とB判それぞ一枚ずつ,合計二枚で,正三角形を作ることもできます。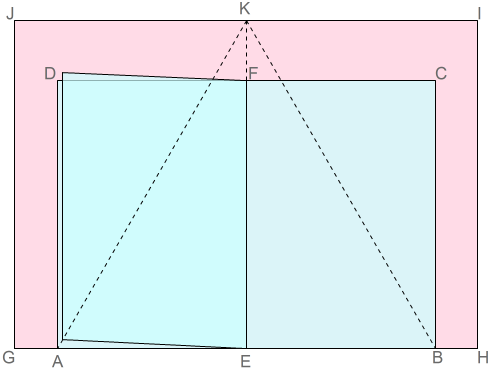 A判とB判は,どのサイズもそれぞれ合同です。二枚を並べると一つ大きいサイズのA判とB判になります。
A判とB判は,どのサイズもそれぞれ合同です。二枚を並べると一つ大きいサイズのA判とB判になります。
大きいサイズを使っても小さいサイズを使っても辺の比は変わりません。操作しやすいサイズの紙を使用するとよいです。
例えば,A5判一枚とB5判一枚,または,A4判一枚とB4判一枚などです。それぞれを長辺で半分に折って折り目を並べると,先と同じように正三角形の頂点を確定できます。
□ABCDを,長辺を2等分する直線FEで折って,折り目をつけて開きます。同様に,B判GHIJを,直線EKに折り目をつけて開きます。EFをEKの上に乗せ,□ABCDの長辺HGをB判GHIJの長辺GHの上に乗せます。そして,頂点Eが一致しているか確かめます。
このとき,GH上の点Aと点B及び点Kは正三角形ABKの三つの頂点になっています。
(3)解説
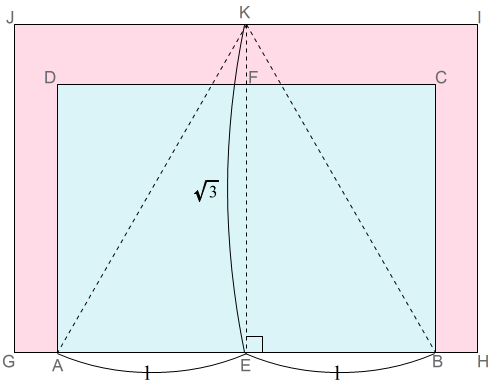
A4判紙の頂点Bに四枚の紙の頂点を合わせて図のように重ねて並べます。そのときできる三角形ABKは正三角形です。
三角形AEKは,\[∠AEK=∠R\] なので,直角三角形です。したがって,三平方の定理と \(AE=1,EK=\sqrt{3}\) より,
$$\begin{equation}\begin{split}AE^2+EK^2&=AK^2\\1^2+\sqrt{3}^2&=AK^2\\AK^2&=1+3\\AK&= \sqrt{4}\\&=2\end{split}\end{equation}$$
したがって,\(AE=BE=1\) から,\(AB=AK=BK=2\) なので,三つの辺が等しい三角形となります。すなわち三角形ABKは正三角形といえます。
以上の正三角形を作る方法は,同サイズ同番号のA判二枚とB判二枚を各短辺と長辺を一頂点に揃え並べて正三角形の頂点を確定する方法です。これは,A判の短辺 1 とB判の長辺\(\sqrt{3}\),A判B判の長方形が合同であることを利用した作図方法です。
4 \(\dfrac{1}{2}\) 対角線と垂直二等分線 その1
(1)見方・考え方
A判一枚の中に正三角形を作ることを考えます。垂線の長さを移す道具の作成用に別に一枚用意します。
正三角形の高さは,\(\sqrt{3}\) です。 前の作り方では,B判の長辺 \(\sqrt{3}\) を利用して,それを高さとする正三角形を作りました。
前の作り方では,B判の長辺 \(\sqrt{3}\) を利用して,それを高さとする正三角形を作りました。
\(\sqrt{3}\) の長さは他にもあります。下左図のようなA判の対角線です。
A判・B判はともに相似なので,単体の辺の比は,短辺:長辺:対角線\(=1:\sqrt{2}:\sqrt{3}\) です。
ここでは,A判の短辺を 1 としているので,正三角形の作成に必要な 1 と \(\sqrt{3}\) の長さはA判にあります。
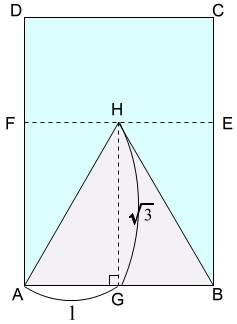 まず,□ABCDに正三角形ABHが描けたとします。
まず,□ABCDに正三角形ABHが描けたとします。
正三角形ABHは,ABを一辺とするので,3頂点のうち2頂点A,Bは決まります。残るは,3頂点目の頂点Hです。それが決まれば正三角形ABHを作れます。
ここでは,ABの垂直二等分線上に高さをとる方法を考えましょう。垂直二等分線は,紙を半分に折ればすぐに作れます。あとは高さを作って移すだけで済みます。 そこで,高さが必要です。\(AB=1\) とするときの高さです。
そこで,高さが必要です。\(AB=1\) とするときの高さです。
$$\begin{equation}\begin{split}AM:AH:MH&=1:2:\sqrt{3}\\MH&=\sqrt{3}AM\\&=\sqrt{3}\times \dfrac{1}{2}AB\\&=\sqrt{3}\times \dfrac{1}{2}\\&=\dfrac{\sqrt{3}}{2}\end{split}\end{equation}$$
したがって,\(AB=1\) とすると,\(MH=\dfrac{\sqrt{3}}{2}\) です。
\(\dfrac{\sqrt{3}}{2}\) は,A判の対角線の半分の長さです。
作図の鍵は,対角線の半分の長さを見つけて移すことです。
(2)作り方
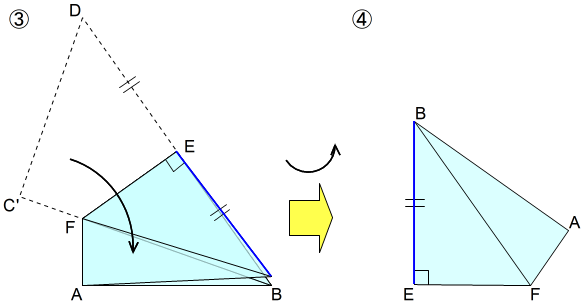
① 対角線で折る
□ABCDを対角線BDで折って,頂点CをC’の位置に折り返します。
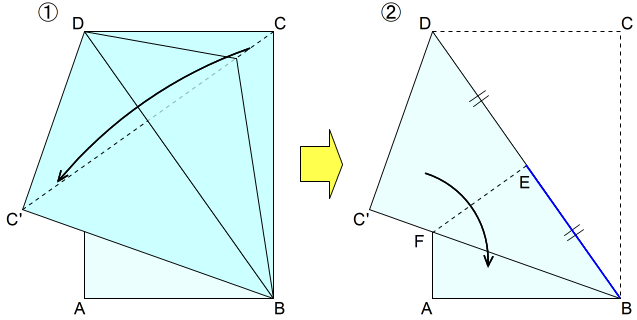
② さらに半分に折る
対角線BDの中点をEとします。頂点Dが頂点Bに重なるように線分FEで折って重ねます。
③ 対角線の半分の長さを作る
半分に折ったとき,頂点C’は頂点Aに一致します。できる長さBEは,対角線の半分です。
④ \(\dfrac{\sqrt{3}}{2}\) の垂線を作る
垂線BEは,\(EF\perp EB,EB=\dfrac{\sqrt{3}}{2}\)です。正三角形の底辺の中点から,底辺に対する頂点を確定するときに,これを道具として使います。これを「道具」と呼ぶことにします。
⑤ 短辺を2等分する折り目を入れる
道具とは別のA判を用意し,それを短辺を2等分するよう半分に折って,A判に折り目を入れます。
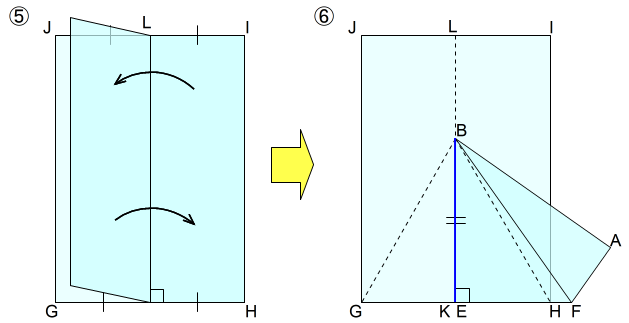
⑥ 道具を合わせる
A判GHIJの短辺GHの中点をK,短辺JIの中点をLとします。道具の頂点Eを中点Kに合わせ,A判のKHと道具のEFが重なるように,道具をA判に配置します。
このとき,道具の頂点Bは,正三角形GHBの辺GHに対する頂点です。
(3)解説
道具は,A判の対角線の半分の長さで作っています。したがって,道具は,垂線の長さ\(EB=\dfrac{\sqrt{3}}{2}\)を与えます。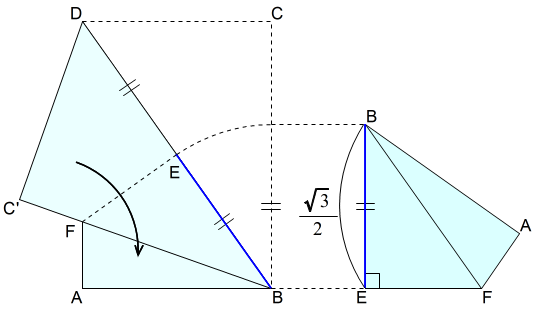 上の正三角形の作り方では,道具を使って,□ABCDに垂線の長さを移します。
上の正三角形の作り方では,道具を使って,□ABCDに垂線の長さを移します。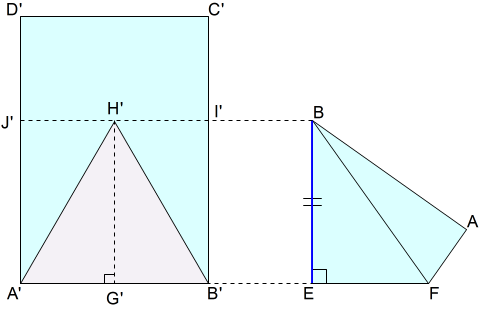
三角形A’G’H’と三角形B’G’H’において
\(A’G’=B’G’=\dfrac{1}{2},∠A’G’H’=∠B’G’H’=∠R,G’H’=\dfrac{\sqrt{3}}{2}\)共通 より,二つの三角形の二辺挟角が等しいので,
\(\bigtriangleup A’G’H’ \equiv \bigtriangleup B’G’H’\)
したがって,\(A’H’=B’H’=A’B’=1\) となり,三角形A’B’H’は正三角形といえます。
また,その大きさは,一辺の長さが 1,高さが\(\dfrac{\sqrt{3}}{2}\) の正三角形です。
以上の正三角形を作る方法は,垂直と対角線の\(\dfrac{1}{2}\)の長さをもつ道具を使って,短辺の垂直二等分線に頂点をとる方法です。これは,A判の対角線の \(\dfrac{1}{2}\) が \(\dfrac{\sqrt{3}}{2}\) であること,正三角形の頂点が対辺の垂直二等分線上にあることを利用した作図方法です。
5 \(\dfrac{1}{2}\) 対角線と垂直二等分線 その2
(1)見方・考え方
前の例では,垂線の長さ \(EB=\dfrac{\sqrt{3}}{2}\) を移す道具を作成しました。せっかくその長さをA判はもつので,同じ一枚の中で完結させることを考えます。
適切な場所に \(\dfrac{\sqrt{3}}{2}\) の長さを移して,A判に直接正三角形を作ります。道具の垂線は,対角線の一部です。だから,同じA判内の短辺に垂直な長さを移す必要があります。
(2)作り方
「4 \(\dfrac{1}{2}\) 対角線と垂直二等分線 その1(2)作り方③」までは,道具の作り方と同じです。
④ BEをBE’に移す
BEとBFが重なるようにBGで折ります。BGを対象の軸として点Eを対称移動します。点Eと線対称でBF上の点をE’とします。
⑤ 長さ \(\dfrac{\sqrt{3}}{2}\)の垂線を作る
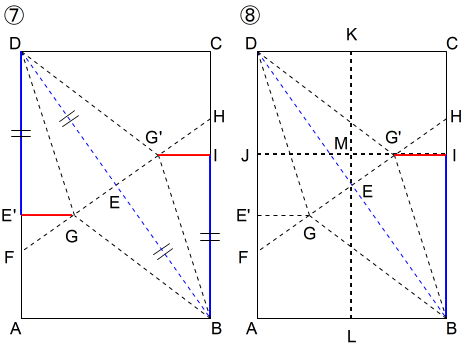
\(∠BEG=∠BE’G=∠R\)なので,線分GE’で折ります。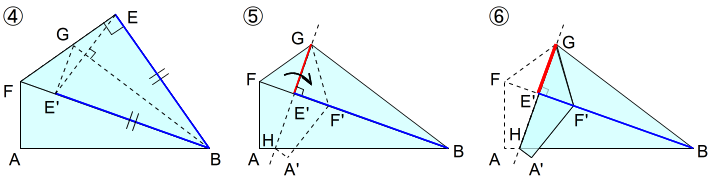 ⑥ 垂線の折り目を入れる
⑥ 垂線の折り目を入れる
点Fを点F’までGHを対象の軸として線対称移動する位置で,折り目を入れます。このとき,必要な折り目は,赤い部分のみです。線分GE’が分かるように折り目を入れます。
⑦ A判を開いて折り目を確かめる
線分GE’の折り目を入れたことで,二箇所に折り目が残ります。
\(GE’\perp DE’,BI\perp G’I,E’D=BI\)です。
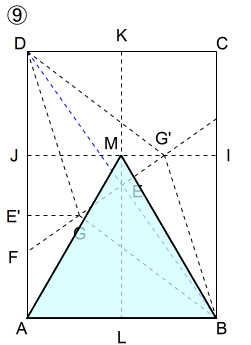
 ⑧ \(LM=\dfrac{\sqrt{3}}{2},JM=IM\)となる頂点Mをとる
⑧ \(LM=\dfrac{\sqrt{3}}{2},JM=IM\)となる頂点Mをとる
G’Iを延長した辺ADとの交点をJとします。IJでA判を折って折り目を入れます。次に,短辺を2等分する線分KLで折って折り目を入れます。IJとKLの交点をMとします。
⑨ 三角形ABMが正三角形
点Mが正三角形のABに対する頂点です。三点ABMを線分で結ぶと正三角形ができます。
(3)解説
三角形ABMは正三角形です。
三角形ALMと三角形BLMにおいて
\(AL=BL=\dfrac{1}{2},∠ALM=∠BLM=∠R,LM\)共通 より二辺挟角が等しいで
\(\bigtriangleup A’G’H’ \equiv \bigtriangleup B’G’H’\)
また,三角形ALMは直角三角形です。このことから三平方の定理が成り立ちます。
作図方法より,\(LM=IB=E’D=BE=DE=\dfrac{\sqrt{3}}{2}\) であることから,
$$\begin{equation}\begin{split}AL^2+LM^2&=AM^2\\\dfrac{1}{2}AB^2+\left( \dfrac{\sqrt{3}}{2} \right)^2&=AM^2\\AM^2&=\dfrac{1}{4}+\dfrac{3}{4}\\&=1\\AM&=1\end{split}\end{equation}$$
したがって,\(AM=BM=AB=1\) となり,三角形ABMは正三角形といえます。
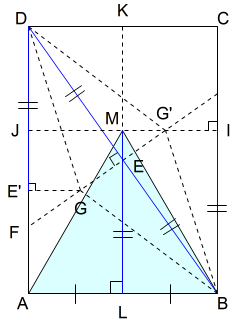
以上の正三角形を作る方法は,一枚のA判に,対角線の\(\dfrac{1}{2}\)の長さを長辺に移して高さを決め,短辺の垂直二等分線上に頂点をとる方法です。これは,A判の対角線の \(\dfrac{1}{2}\) が \(\dfrac{\sqrt{3}}{2}\) であること,正三角形の頂点が対辺の垂直二等分線上にあることを利用した作図方法です。
6 まとめ
A判の短辺を 1 とすると,同一番号のA判の短辺と長辺,B判の短辺と長辺の比は,次のようです。
$$1:\sqrt{2}:\sqrt{\dfrac{3}{2}}:\sqrt{3}$$
A判・B判は互いに相似で,単体の短辺と長辺と対角線の比は,次のようです。
\[=1:\sqrt{2}:\sqrt{3}\]
正三角形は,3つの辺がすべて等しい三角形です。それを2分割した一つの直角三角形の辺の比は,\(1:2:\sqrt{3}\) です。
正三角形の一辺を垂直に2等分すると,垂直二等分線は対する頂点を通り,2つの合同な直角三角形に分割できます。
これらの定義や性質を使って,A判,B判で正三角形を作る方法として,以下の四つを紹介します。
1 短辺で二つ折りにして,折り目上に短辺の一つの端点から短辺と等しい長さの点を取って作る方法です。これは,短辺と垂直二等分線を使った方法であり,正三角形を2等分する合同な直角三角形の性質を利用した作図方法です。
2 同サイズ同番号のA判二枚とB判二枚を各短辺と長辺を一頂点に揃え並べて正三角形の頂点を確定する方法です。これは,A判の短辺 1 とB判の長辺 \(\sqrt{3}\),A判B判の長方形が合同であることを利用した作図方法です。
3 垂直と対角線の \(\dfrac{1}{2}\) の長さをもつ道具を使って,短辺の垂直二等分線に頂点をとる方法です。これは,A判の対角線の \(\dfrac{1}{2}\) が \(\dfrac{\sqrt{3}}{2}\) であること,正三角形の頂点が対辺の垂直二等分線上にあることを利用した作図方法です。
4 一枚のA判に,対角線の\(\dfrac{1}{2}\)の長さを長辺に移して高さを決め,短辺の垂直二等分線上に頂点をとる方法です。これは,A判の対角線の\(\dfrac{1}{2}\) が \(\dfrac{\sqrt{3}}{2}\) であること,正三角形の頂点が対辺の垂直二等分線上にあることを利用した作図方法です。