- 平成30年度全国学力・学習状況調査では,「数学的な見方」に関わる問題が出題されたのでしょうか。
- ピタゴラスの定理の発見にもつながる数学的な見方を促す問題が出題されました。
調査問題は,「うろこ模様」を調べる場面から始まり,ひし形や台形,正三角形を例として,平行四辺形を見出す問題です。
このような敷き詰め模様から図形を見出し,図形の性質や図形相互の関係を考察する話合い活動は,「主体的・対話的で深い学び」の実現につながります。
1 ピタゴラスの定理の発見につながる学力テストの問題
昨日の4月17日(火)に,平成30年度全国学力・学習状況調査が全国の小中学校で実施され,早速,今朝の新聞に調査問題が公表されました。
その中の小学校算数B問題に,興味ある面白い問題を見つけました。ピタゴラスの定理の発見につながる「数学的な見方」を促す問題です。
「見えますか?タイルの模様からピタゴラスの定理」
 ピタゴラスは,寺院の床のタイルを見て,その模様からピタゴラスの定理を発見したと伝えらています。
ピタゴラスは,寺院の床のタイルを見て,その模様からピタゴラスの定理を発見したと伝えらています。
その例のように,図形を考察する際は,図形の形や量に着目します。
図形の形や広がり,そして辺や角,頂点といった構成要素の特徴や性質,それらの関係,角の大きさ,長さや面積という量の特徴や性質,それらの関係などです。
今回の調査問題では,敷き詰められた図形を考察する問題が出題されました。
2 うろこ模様は図形の敷き詰め
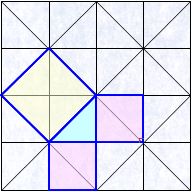
調査問題は,「うろこ模様」を調べる場面から始まります。
うろこ模様は,二等辺三角形を一つの単位として幾何学的な連続文様を上下左右につないでつくります。
その形状が魚鱗を思わせるところから名づけられたと考えらます。
単位となる図形は,正三角形や二等辺三角形,半円などがあります。
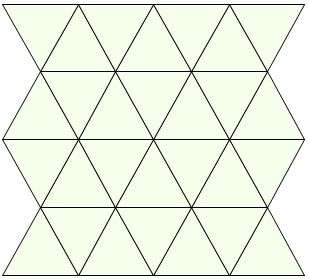
さて,先ほどのうろこ模様の図形に戻ります。
このうろこ模様は,美しい模様です。一見すると,単なる規則的な模様です。
よく見ると,一つ一つの図形は合同です。
単位となる図形は,正三角形です。
「合同な正三角形が敷き詰められているから,美しく見える。」と改めて気付かされます。
敷き詰めている図形の辺や角の組み合わせを変えて見ると,違う図形が見えてきます。
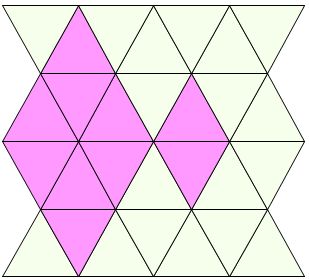 まず,ひし形。
まず,ひし形。
ダイヤモンドのようです。
2二枚使った小さいひし形。
8枚使った大きいひし形。
大きいひし形が連なっているようにも見えます。
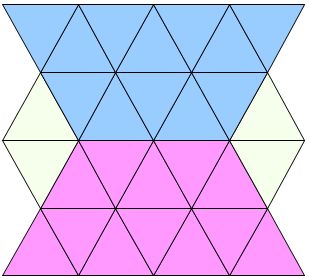 台形も見えます。
台形も見えます。
3枚使った台形。
8枚使った台形。
15枚使った台形も見いだせす。
12枚使った台形が上下逆さになって重なっているようにも見えます。
7枚の台形が上下に逆さまになって4段に積み重なってるようにも見えます。
当然正三角形が見えます。
単位の正三角形の他に,4枚の正三角形。
9枚の正三角形。16枚の正三角形も見えます。
16枚の正三角形は,上下に逆さまになり,部分を共有して見えます。そこには幾何学的な面白さがあります。
他にも,小学校で学ぶ基本図形が見えます。
これが,全国学力・学習状況調査の問題としての問いかけです。
「他に正三角形4つでできる図形はないか。」
調査問題ですから,採点等の都合上,「正三角形4つ」と条件は限定します。
もしこれを授業の教材とするなら,子どもたちに多様に考えさせたいところです。
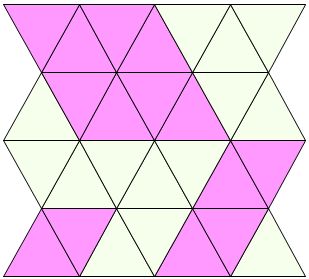 調査を実施した小学校第6学年の子どもたちならば,
調査を実施した小学校第6学年の子どもたちならば,
平行四辺形は発見するでしょう。
小さいものでは,2枚でできます。
そういえば,先ほどのひし形も2枚でした。
ここで気付きます。
2枚のひし形と2枚の平行四辺形は,同じ。
ひし形と平行四辺形は等しい図形なのか,仲間なのか。
どちらかが特殊なのか。
ここで,子どもたちの話合いです。
6年生にとっては既習の内容なので,その後の話合いでは集合の包摂関係を確認することになります。
さて,戻ります。平行四辺形は,他にも見えます。
4枚でも,6枚でも,8枚でも見ます。
12枚でも,16枚でも見えます。
このように,うろこ模様の中から,いろいろな図形を見ることができます。
3 数学的な思考力・判断力・表現力,数学的な態度への問い
授業であるなら,子どもたちの問いは続きます。
教師は,アンテナを鋭敏にして,子どもたちの意識の流れをつかんで表舞台に出す必要があります。
| 「そもそも,どうして図形を見つけられたのか。」 |
これは,数学的な見方への問いです。
図形の構成要素や図形の性質に着目する必要性を明確にします。
| 「なぜ,ひし形,台形,正三角形,平行四辺形と判断したのか。」 |
これは,数学的な判断力への問いです。
図形の定義や性質に照らして判断することを明確にします。
| 「なぜ,うろこ模様は美しく見えるのか。」 |
これは,図形の美しさに関わる数学的な態度への問いです。
幾何学的な図形そのものの美しさ,図形の対称性や規則性などに気付くようにします。
これらの問いの根拠を考えるのが数学的な思考力であり,考える方向を示すのが,数学的な考え方です。
そして,判断の根拠を示して説明するのに必要なのが,数学的な表現力です。
理由の説明には,当然に用語が必要です。辺や角などの図形の構成要素等の正確な知識が必要です。
また,図形の性質の理解を基に,平行な辺の組の数に着目する数学的な見方を働かせたことを説明する必要があります。
このような問いについて考え表現する学習活動を通して,子どもたちが話し合い確かな結論を見出すことは,「主体的・対話的で深い学び」の実現につながります。
加えて,図形の美しさ,対称性の美しさも話題にしたいところです。
そのことによって,数学的な態度の一つである幾何学的な図形の美しさという見方や感性を育てることができます。
4 調査問題から授業改善
敷き詰められた模様の中に,いろいろな図形を見ることができます。
「うろこ模様の中に,図形を見る。」
これが,図形の構成要素に着目する数学的な見方の一つです。
上記の問題設定は,数学的活動としてみれば,日常の事象の数学化の学習過程に当たる問題といえます。
数学的活動とは,「事象を数理的に捉え,算数の問題を見いだし,問題を自立的,協働的に解決する過程を遂行すること」です。
児童の問題発見や問題解決の学習過程としては,「日常生活の事象を数理的に捉え,数学的に表現・処理し,問題を解決したり,解決の過程や結果を振り返って考えたりする」ことに当たります。
このようなことをねらいの一つとして問う問題が,全国学力・学習状況調査で出題されました。このことは,日常の事象を数学的な見方を働かせ問題を見出す指導の必要性を示しています。
新学習指導要領では,「見方・考え方」を,算数科・数学科では数学的な見方・考え方働かせることを重視しています。
今後,数学的な見方・考え方をより一層明確にして,子どもたちがそれらを身に付け「働かせる」ことができるようにすることが大切です。