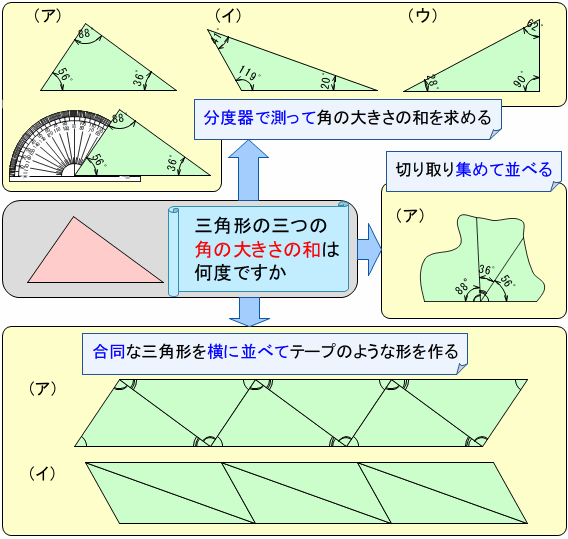
- 関数の考えを学ぶよさは何でしょう。関数の指導は,どこがポイントでしょう。
- 関数の考えを学ぶよさは,日常生活の中である事象を直接に調べられないとき,関数関係にある他の数量の規則を利用して,もとの事象の問題解決を図ることができるところにあります。
関数の指導では,以下の指導のポイントがあります。
① 決まりを見付ける考え方
・ 依存する数量を見つける
・ 数量の関係を見つける
・ 数量の関係を使って問題を解決する
② 決まりが見つからないときは,「変化の決まり(法則)」に着目する
・ 対応の決まりが分からないとき「変化の決まり(法則)」に着目する,
・ 変化の決まりを見付けやすいように,表やグラフに表す,
・ 数量の関係を,関数の考えで積極的に見る・考える
③ 関数の考えで積極的に見ると解決できる体験やうまく問題解決する体験を重ねる
1 関数の考えの指導の変遷と学ぶよさ
(1)関数の意味の理解に象徴される1960年代
今から50年ほど前1960年代は現代化運動が盛んでした。
それは,1957年昭和32年に,ソ連の人工衛星スプートニク1号が打ち上げられたことが大きな要因でした。
これを契機に,数学・自然科学教育のカリキュラムを改造する運動が急速に広がりました。
その頃の関数の内容は,1958年昭和33年小学校学習指導要領では,「C数量関係」の領域は「割合」「式・公式」「表・グラフ」で構成され,関数は「割合」の中で取り扱いました。

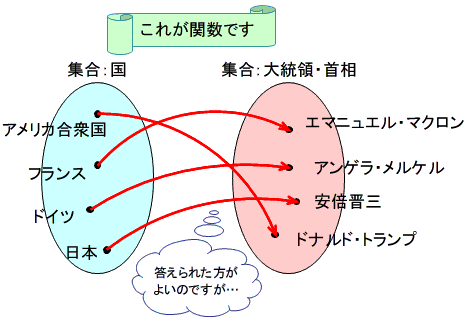
実際の関数指導では,「ドイツの首都はどこですか。」「ベルリンです。」という内容でした。
「国」の集合に「首都」の集合を対応させ,「国と首都が関数」と言うだけの知識でした。
当時の考え方は,科学の体系性を重視するあまり,子どもの経験や問題意識を軽視する傾向にありました。
数学的には,「関数」は「関係」の中に含まれ,一対一対応の「関係」を言います。
ですから,一つの要素(国名)がただ一つの要素(首都)に対応するという数学の世界の概念がそのまま指導されていた状況でした。
(2)問題解決に生かす「関数」「関数の考え」
その後,1971年昭和46年小学校学習指導要領では,「D数量関係」の領域は「関数」「式表示」「統計」で構成され,3年生から「関数」が指導されました。
内容を充実させ,関数の指導の重要性が高められました。
昭和33年では,
「比例の考え方を…用いる能力を伸ばす」
昭和46年では,
「比例関係に着目して考察すると能率よく処理できる事象が多いことを知ること」
平成20年では,
「比例の関係を用いて,問題を解決すること」
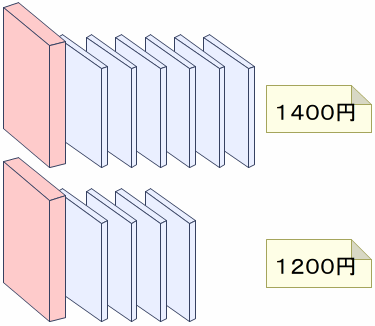
平成20年の学習指導要領に基づく教科書では,例えば,束にした針金の長さは重さとの関数であることから,針金の束の重さを調べて針金の長さを求めるなど,関数の考えが問題解決に生かされるようになりました。
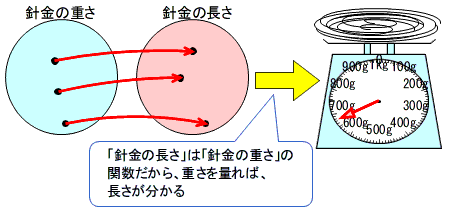 このように,関数の考えを使って合理的に問題を解決できるようにする,学んだことが生きて働くようにする指導へと変わってきました。
このように,関数の考えを使って合理的に問題を解決できるようにする,学んだことが生きて働くようにする指導へと変わってきました。
関数の考えを学ぶよさは,日常生活の中である事象を直接に調べられないとき,関数関係にある他の数量の法則を利用して,もとの事象の問題解決を図ることができるところにあります。関数の考えを必要な時に活用できるようになれば,手間をかけずに合理的に問題の解決を図ったり,手際良い処理ができたりすることが考えられます。
(3)平成29年改訂学習指導要領で領域「変化と関係」の新設
平成29年改訂小学校学習指導要領では,変化や関係を把握する力の育成の重点化と統計教育の充実を図りました。
従前の「数量関係」は,主として,関数の考え,式の表現と読み,及び資料の整理と読みの三つの下位領域からなるものでした。今回の改訂により,従前の「数量関係」の内容を新たに設けた「変化と関係」と「データの活用」に移行しました。これにより,数量の変化や関係に着目した考察を重視するとともに統計教育の基礎を充実することとしました。
① 「変化と関係」を上学年に新設
「変化と関係」の領域の新設については,算数科で育成を目指す資質・能力の重要な事項に,事象の変化や関係を捉えて問題解決に生かそうとすることがあり,これが従前から「関数の考え」として重視されてきたことを踏まえています。今回の改訂では,事象の変化や関係を捉える力の育成を一層重視し,二つの数量の関係を考察したり,変化と対応から事象を考察したりする数学的活動を一層充実するために,従来の「数量関係」領域の考え方を生かすものとして,上学年に設けました。この領域の内容は,中学校数学の「関数」領域につながるものであり,小学校と中学校の学習の円滑な接続をも意図しています。
② 下学年は「関数の考え」の素地指導
なお,「変化と関係」領域を上学年に位置付けたのは,従来の「数量関係」の領域における「関数の考え」が育成される内容が,伴って変わる二つの数量の関係(第4学年),簡単な比例(第5学年),比例と反比例(第6学年)など,上学年に位置付けられていたことを踏まえたものです。しかしながら,下学年においても,数や図形の等の考察において,数の関係を考察したり,変化の規則に注目したりする場面が多いことに注意が必要であり,そのような場面は「関数の考え」の素地指導をする重要な機会です。
2 関数の考えを生かす指導
関数は,本来は法則を知って,問題が処理できる予測できるようにするために使うものです。
関数の指導は,関数そのものの指導ではありません。グラフをかくとか,関数そのものが分かることは大切です。
ですが,関数の考えを利用して仕事ができることを学ぶことは,もっと大切です。
現行学習指導要領では,「関数の考え」を生かす指導は以下のようになっています。
1. ある場面での数量や図形についての事柄が,ほかのどんな事柄と関係するかに着目する
2. 二つの事柄の変化や対応の特徴を調べていく
3. 見いだした変化や対応の規則性を,様々な問題の解決に活用し,その思考過程や結果を表現したり,説明したりする
このように,数学的な見方・考え方を発揮しながら問題解決ができるようにすることが大切です。
3 関数の指導の具体
関数の指導の具体的な指導のポイントは,円の面積の求め方の指導を例にすると以下のようです。
(1)決まりを見付ける考え方
① 依存する数量を見つける
伴って変わる二つの数量に着目する活動です。
数学的な見方: 一方の数量は,他のどんな数量によって決まるか,依存する関係の数量に着目する。
数学的な考え方: 決まれば決まるのかどうかを考える。
1. 円の面積は,何によって決まるか
求めようとする面積は,図形としての円の面積です。円が決まれば面積は決まります。その円は何によって決まるでしょうか。
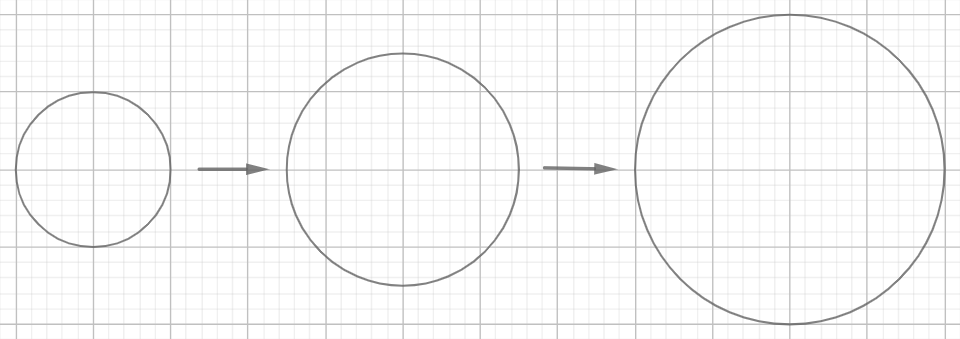
2. 円は,半径で決まる
図形である円は,コンパスで描きます。コンパスの針と開きが円を決めます。中心は,円の位置を決めます。面積に関わるのはコンパスの開き具合です。すなわち半径です。
3. 半径が決まれば,円が決まり,面積が決まる
コンパスの開き具合を決めれば,特定の円が描けます。同時に,円の大きさがきまります。すなわち面積がきまります。
4. したがって,面積は,半径の関数である
コンパスの開きを変えるとそれに伴って描ける円が決まります
開きを大きくするのに伴って,すなわち,半径の長さを長くするのに伴って,円は一意に対応して大きくなり,円の面積がきまります。
このように,円の面積と半径の関係など,伴って変わる二つの数量を見出すことが関数の指導の第一段階です。
② 数量の関係を見つける
関数の指導の第二段階は,伴って変わる二つの数量の関係に着目する活動です。
数学的な見方: 伴って変わる二つの数量の 変化や対応の規則性に着目する。
数学的な考え方:特徴や傾向を見いだすために,関係を,言葉,数,式,表,グラフに表すことを考える。
1. 円の面積と半径は,どんな関係か
円の面積と半径の関係を知りたい 「どんな関係,きまりがあるか」「変わらないものがあるか」
2. 半径という一つの長さで,面積を求めたい
半径と円の面積の関係を,直接調べることは難しそうです。円と似ている,または,関係のありそうな図形はないでしょうか。半径は円を決定する唯一の数量です。この半径一つを使って面積を求めるには,一つの長さで図形・面積が決まる図形に目を向けてみましょう。
3. 一つの長さで面積を求める正方形が,円の求積に使えないか
一つの長さといえば,正方形があります。正方形は,一辺の長さを決めると,一意に正方形が決まります。このことは円と同様です。
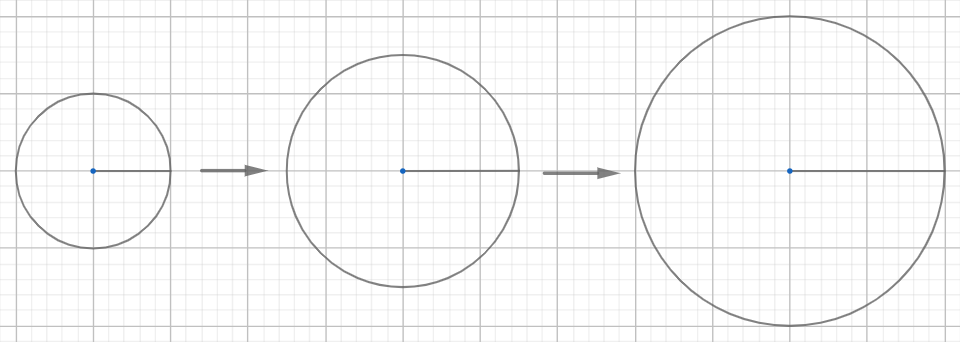
4. 円の面積は,「半径を一辺とした正方形」と関係はないか
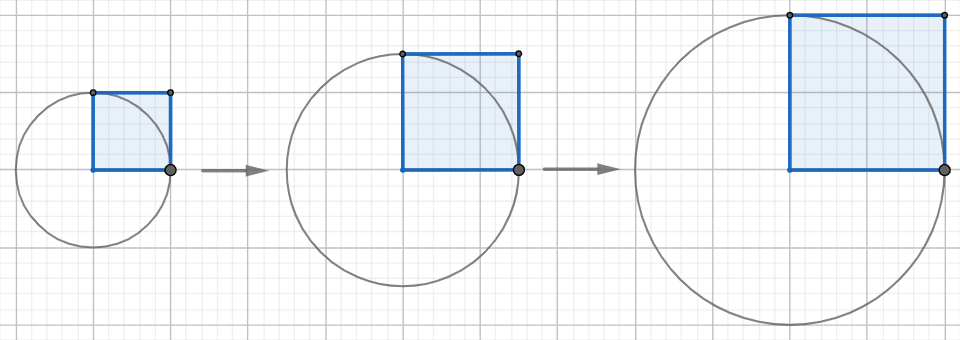
円は半径で決まり,正方形は一辺で決まります。そこで,円とそれに外接する正方形を考えます。半径の長さが変化すれば,それに伴って円と正方形は変化します。伴って変わる変わり方が,円の面積と正方形の面積とでは同じように見えます。
まずは,図にかいたり,方眼紙を使ったりして円の面積と正方形の面積の関係を調べてみましょう。
このように,一辺の長さで決まる図形は何か,これまで学習した図形で使える図形はないかと考えるなど,児童が正方形を必然的に見い出せるようにします。先生が「正方形と比べなさい」と指示するのではなく,このことに児童自ら気付くように授業を工夫したいところです。
そこで,円に外接する正方形や内接する正方形と比較して面積の比の見当を付けたり,方眼のマス目の数の比を求めたり,円をおうぎ形に等分して並べたりする活動をして決まりを調べる活動を設定します。
1. 円の面積と正方形の面積の比を考える
円の面積と正方形の面積の関係について見当をつけます。
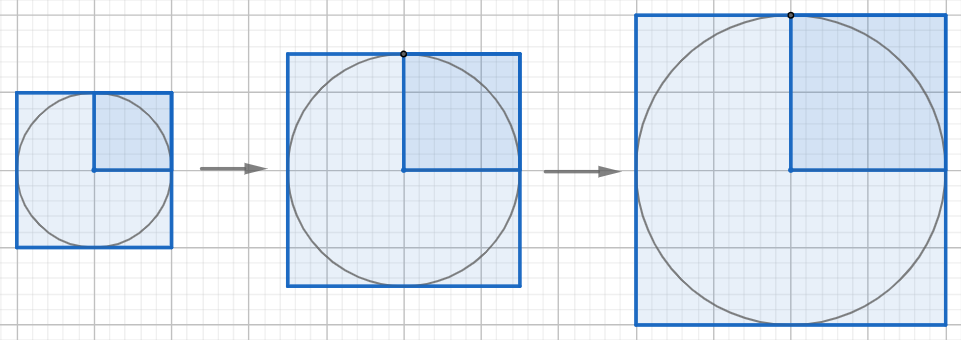
そのために,円の内側(内接)と外側(外接)に正方形を重ねてみましょう。
2. 正方形の面積の約3.1倍
円は曲線で囲まれているので,容易に単位正方形を並べることはできません。そこで,面積の意味に戻り,1cm2の単位正方形が円の中に何個入るかを方眼紙を使って調べます。正方形の方は計算で容易に求められます。得られた数値を使って,比を求めます。
マス目が数えやすいように工夫します。半径10cmにして1/4円の単位正方形のマス目を数えてみましょう。円周にかかる単位正方形は半分とします。
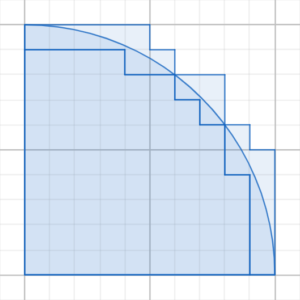 その結果,円の面積は,半径を一辺とする正方形の面積の約3.1倍になります。この比(割合)は,既習の円周率3.14と関係がありそうです。
その結果,円の面積は,半径を一辺とする正方形の面積の約3.1倍になります。この比(割合)は,既習の円周率3.14と関係がありそうです。
3. 円の面積は半径を一辺とした正方形の3.14倍
これで,円の面積は,半径を一辺とする正方形の面積の3.14倍になりそうだという結果の見通しがもてました。
4. 円の面積は,半径×半径の3.14倍
いよいよ円に直接アプローチします。円の面積は分割しても変わりません。幾つかに分割したり位置を動かしたりしても円そのものの面積の大きさは変わらないという量の保存性があります。
そこで,円を半分にして,それぞれをおうぎ形に等分して上下から差し込んで並べてみます。凸凹があり傾向がよく分かりません。さらに,円をもっと細かく等分するとどうなるでしょうか。
細かく等分していくと,おうぎ形を並べた形は長方形に限りなく近づきます。そこで,長方形ができたと仮定します。
すると,できた長方形の縦の長さは半径,横の長さは「円周の半分」です。
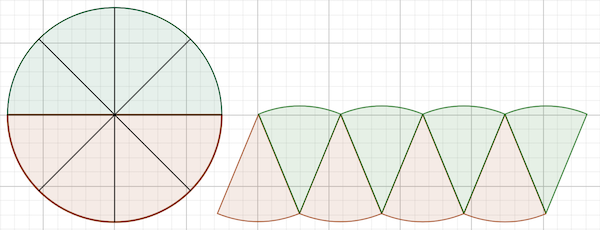
長方形の面積=半径×円周の半分=半径×(直径×円周率÷2)=半径×(半径×円周率)
したがって,円の面積を求める公式は,次のようになります。
円の面積=半径×半径×3.14
このように意識の流れがつながるようにします。児童が主体的に円の面積と半径の関係を見出せるようにすることが大切です。
③ 数量の関係を使って問題を解決する
この公式を利用すると,円の面積を容易に求めることができるようになります。
半径の長ささえ分かれば,円の面積が求められます。
半径が10cmであれば,即座に314cm2と答えられます。
半径が10cmの円の面積=10×10×3.14 答え 314cm2
この場合は複雑な計算を必要としません。
円という図形は,これまで取り扱った図形とは異種の図形で,求積には困難を感じる図形です。
それが,半径の長さと円の面積の関数関係を利用することで簡単に円の面積を求めることができます。
これは,児童にとっては驚きのことと考えられます。
児童がその驚きを体験したり考え方や公式のよさを味わったりできるように,教師が手立てを講じる必要があります。
(2)変化の決まり(法則)に着目する
決まりを見つけようとしても,見つからないことは多いものです。むしろ見つからない方が多いでしょう。
そのようなとき,次のことを考えることが大切です。
① 対応の決まりが分からないとき「変化の決まり(法則)」に着目する
対応の決まりが分からないときは,変化の決まり(法則)に着目します。
一方が変わればもう一方が変わります。一方の変化に対し,他方がどう変化するかという変化の法則ならば,分かるときがあります。
② 表やグラフに表して分かりやすくする
変化の決まりは,数値を表に表すと見付けやすくなります。それをグラフに表すと,変化がもっと分かりやすくなります。
これらの表とグラフを使って,児童が変化の決まりを見出せるようにします。
表やグラフは,関係や法則を調べるためのものです。
変化の決まりが見つかったら,表やグラフの果たした役割を児童に振り返らせ,それらのよさを実感させることが大切です。
③ 関数の考えで積極的に見る・考える
「Aを変えると,Bがどのように変わるかを調べてみよう」
このような見方・考え方を態度化することが,児童の生きて働く力となります。
先生に言われるからではなく,児童自ら考えはじめるよう育てることが大切です。
(3)関数の考えで解決する体験を重ねる
a+b=6
「一方が1ずつ増えたとき,もう一方を1ずつ減らせば,和は変わらない」
という決まりがあります。
この決まりを使って,下記の計算を楽にできないでしょうか。
49+17
被加数49に1を加えて,50にする。
和が1増えるので,加数17から1減らして16にする。
したがって,
49+17=(49+1)+(17-1)=50+16=66
以上述べたように,関数の考えは,それを知ること自体が目的ではありません。
関数や関数の考えを使って問題を解決する体験を重ね,必要なときにうまく問題解決できるようになることが大切なのです。
1 関数の指導は,学んだことが生きて働くようにする。法則を知って問題を処理したり予測したりできるようにする。
2 関数の指導の指導ポイント
(1)決まりを見付ける考え方
① 依存する数量を見つける
② 数量の関係を見つける
③ 数量の関係を使って問題を解決する
(2)決まりが見つからないときは,「変化の決まり(法則)」に着目する
① 対応の決まりが分からないとき「変化の決まり(法則)」に着目する
② 変化の決まりを見付けやすいように,表やグラフに表す
③ 数量の関係を,関数の考えで積極的に見る・考える
(3)関数の考えで積極的に見ると解決できる体験やうまく問題解決する体験を重ねる