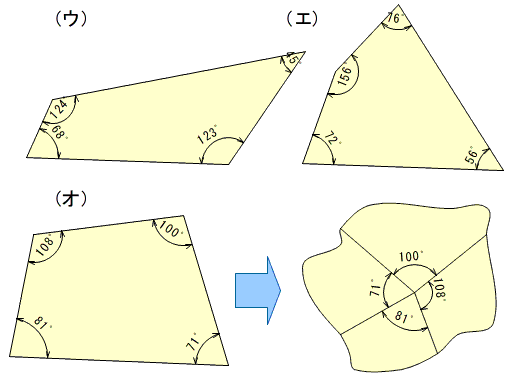
３：４：５の三角形で、本当に直角ができる？

３：４：５の三角形で，本当に直角ができるのでしょうか。
三角形の辺の長さの比と角の大きさには，どんな関係があるのでしょうか。

３：４：５は，斜辺の対角が直角です。このことは，三平方の定理として知られています。
３：４：５の比は，直角を作るため日常的に使われます。
その他にも，５：１２：１３，７：２４：２５，…などの整数比があります。
辺の長さの比が１：１：１の正三角形では６０°，角の二等分線で３０°，３：４：５の直角三角形では９０°，この直角三角形を利用して直角をつくる辺を等しくすると４５°が，容易に作れます。
【参考】
１：２：２ の三角形　→　二等辺三角形で，頂角約２９°，底角約７６°
２：２：３ の三角形　→　二等辺三角形で，頂角約９７°，底角約４１°
２：３：４ の三角形　→　約１０４°，約４７°，約２９°








１　直角三角形の性質の利用

「類推の精度を高める数学的見方」で，次の問題を提示しました。教材となる平行四辺形は，斜辺５ｃｍ高さ４ｃｍです。

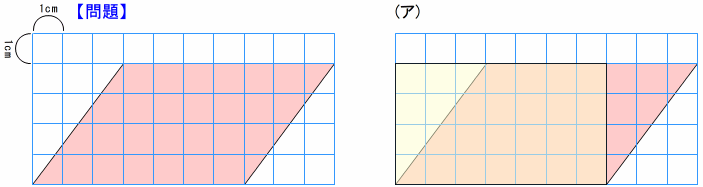
問題には，斜辺５ｃｍ高さ４ｃｍの平行四辺形を提示します。

この問題では，児童の話合いを深めるきっかけをつくるため，斜辺を整数値になるように決めています。
この決め方は，もう一辺の長さが３ｃｍの直角三角形の性質を利用しています。
３ｃｍ，４ｃｍ，５ｃｍという組み合わせの直角三角形は，児童が，算数のノートに長さを測り取って作図するのに，ちょうどよい大きさです。
考えを書き込むスペースが必要なノートに，図形が収まりやすく，児童が作図しやすいサイズで，３辺が整数値になる直角三角形はこれ一つです。

２　三平方の定理（ピタゴラスの定理）

（１）三平方の定理

この直角三角形の３辺の関係の性質は「三平方の定理」として中学校第３学年で指導します。

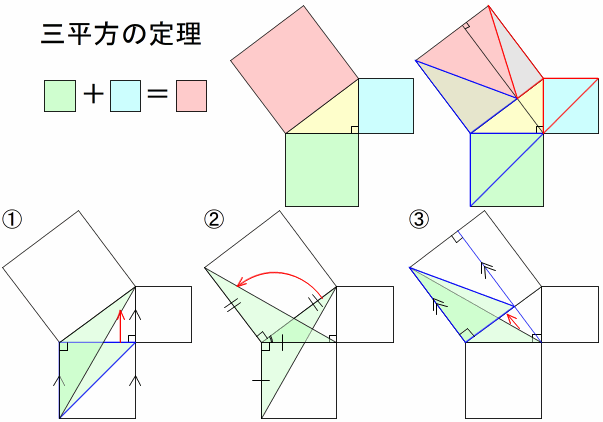
①　底辺と平行な直線上を頂点が移動し高さが等しいため，三角形の面積は変わらない。
②　合同な三角形は面積が等しい。
③　①と同様

ピタゴラスの定理の証明方法は数百通りあることが知られています。

中学校の教科書では，図形の性質を使った証明は発展的な学習で取り扱われ，数式を中心とした証明を取り扱っています。

Ｒ＝（ａ＋ｂ）^２－（１／２）ａｂ×４
＝ａ^２＋２ａｂ＋ｂ^２－２ａｂ
＝ａ^２＋ｂ^２
Ｐ＝ａ^２，Ｑ＝ｂ^２
∴Ｐ＋Ｑ＝Ｒ

したがって，
３：４：５の比の場合
３^２＋４^２＝９＋１６＝２５＝（√２５)^２＝５^２
５：１２：１３の比の場合
５^２＋１２^２＝２５＋１４４＝１６９＝（√１６９）^２＝１３^２

他にも，７：２４：２５，…などの整数比があり無数に存在します。

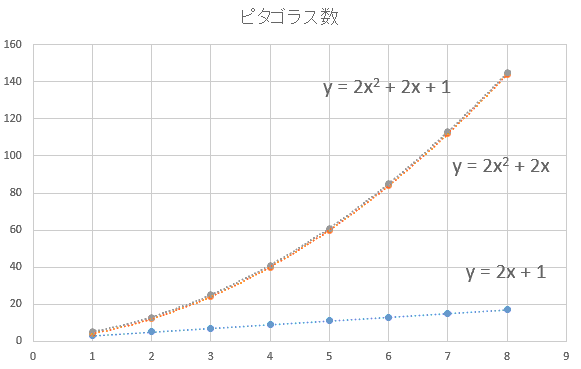
（２）ピタゴラス数

（３，４，５）（５，１２，１３）（７，２４，２５）のような直角三角形の３辺の長さとなる自然数の組を，「ピタゴラス数」といいます。
最大公約数が１のピタゴラス数は，異なる自然数ｍ，ｎを用いて次のように表されることが知られています。

ｘ＝ｍ^２－ｎ^２，ｙ＝２ｍｎ，ｚ＝ｍ^２＋ｎ^２

ｍ＝２，ｎ＝１のとき，ピタゴラス数（３，４，５）　このとき，なんと面積は「６」
ｍ＝３，ｎ＝２のとき，ピタゴラス数（５，１２，１３）
ｍ＝４，ｎ＝３のとき，ピタゴラス数（７，２４，２５）

ピタゴラス数に関わって，フェルマーの最終定理というものがあります。

「フェルマーが驚くべき証明を得たと書き残したと伝えられ，長らく証明も反証もなされなかったことからフェルマー予想とも称されたが，３６０年後にアンドリュー・ワイルズによって完全に証明され，ワイルズの定理あるいはフェルマー・ワイルズの定理とも呼ばれるようになった。」
ウィキペディア「フェルマーの最終定理」[online]https://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A7%E3%83%AB%E3%83%9E%E3%83%BC%E3%81%AE%E6%9C%80%E7%B5%82%E5%AE%9A%E7%90%86(2017/5/31)
フェルマー・ワイルズの定理によれば，（ｎ＝３）：ｘ^３＋ｙ^３＝ｚ^３となる自然数の組（ｘ，ｙ，ｚ）は存在しません。
ｘ＝ｍ^２－ｎ^２，ｙ＝２ｍｎ，ｚ＝ｍ^２＋ｎ^２で求められる（ｎ＝２）：ｘ^２＋ｙ^２＝ｚ^２は，三平方の定理です。
（ｎ＝１）：ｘ＋ｙ＝ｚは（２，１，３）など無限に存在します。

このように考えてくると，（ｎ＝１）は特段の意味をもたず，（ｎ>=３）は存在しないので，（ｎ＝２）：ｘ^２＋ｙ^２＝ｚ^２が重要です。
その中でも，ピタゴラス数（３，４，５）は，特異な自然数の組と考えられます。
ピタゴラスの定理が有用なのは，定理の逆も成り立つからです。

ピタゴラス数（３，４，５）を使って直角をつくる場面は，生活の中で見ることができます。








３　三角形の辺の比の利用

（１）３：４：５の利用

①　運動場に直角をつくる

学校では，運動場に直角を作る必要のあるとき，巻き尺を３：４：５の比にして直角を作ることがあります。
ピタゴラスの定理の逆を利用しています。

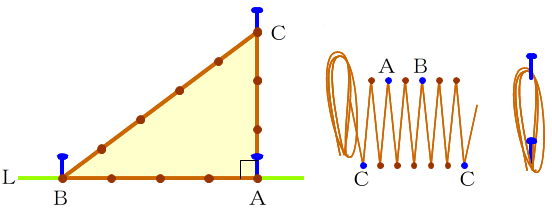
1. まず，直角をなす一辺となる直線Ｌを決めます。
2. 直線Ｌ上に基準点Ａを取り，釘Ａを打ちます。点Ａを頂点として直角を作ります。
3. 直線Ｌ上に基準点Ａから４ｍのところを点Ｂとし２本目の釘Ｂを打ちます。
4. ２つの釘ＡＢにロープ（巻尺）をひっかけながら， ０ｍと１２ｍの目盛りを重ねて保持し，ロープをぴんと張ります。そのとき，辺ＡＣは３ｍ，辺ＡＢは４ｍとなるよう点Ａと点Ｂの目盛りがずれないようにします。重ねて保持した点を点Ｃとし釘Ｃを打ちます。
5. このとき，三角形ＡＢＣは直角三角形です。はじめに打った釘Ａを頂点とする角ＢＡＣが直角になります。

直角作りとを通して，３辺の長さが決まれば三角形が一意に決まることを実感できます。

続いて，４５°を作ります。

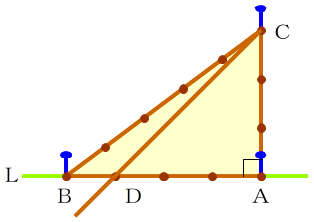
1. 辺ＡＢ上で，点Ａから点Ｂに向かって３ｍの点を点Ｄとします。
2. ３本の釘を利用して，ギリシャ文字φの小文字の筆記体を書くように，点Ｃ→点Ｂ→点Ａ→点Ｃ→点Ｄとロープを釘にかけながら伸ばします。
3. 点Ｃから点Ｄを通る直線を作ります。
4. このとき，角ＡＣＤの大きさは４５°です。
5. 辺ＡＣ＝辺ＡＤなので，三角形ＡＣＤは直角二等辺三角形です。したがって，角ＣＤＡの大きさも４５°です。

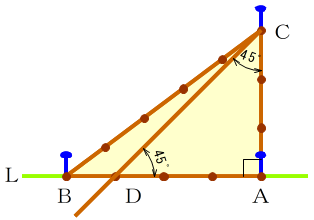
②　建設現場で直角を確かめる

建設現場でも，直角を確かめるときに使われるときがあります。

1. 直角と思われる二本の交わった線の一辺に鉛筆等で３ｍの印を付けます。
2. もう一辺を４ｍの印を付けます。
3. 印と印の長さを測って５ｍなら，
4. この二本の交わった線は直角と判断します。

③　日常で３：４：５を作る方法

日常では，直角は容易に作れます。巻き尺などの普遍単位のメジャーは必要ありません。

1. 長めのひもやロープを用意します。
2. 任意に１の単位の長さを決めます。直角を利用する図形が大きいときは，単位を長めに取ります。長めの時は一ひろ分（自分の体で，両手を広げた長さ）が容易に作れます。ただし，一ひろで単位の長さをとると，２０ｍほどのひもが必要になります。
3. ３ひろ，４ひろ，５ひろの長さのところに印を入れます。印が入れられないときは，結び目（バタフライノットなど）を作ります。
4. 印を入れたところに３点を固定すれば，斜辺５に対応する角の大きさが直角になります。

（２）その他の辺の長さの比と角大きさの関係

①　１：１：１，２：２：(１+１)の利用

辺の長さの比が１：１：１の三角形，すなわち正三角形では，一つの角の大きさが６０°です。これは最も容易に作図できます。
この応用として，２：２：(１+１)の利用ができます。正三角形の一つの角の二等分線を作図すると，その角の大きさは３０°です。
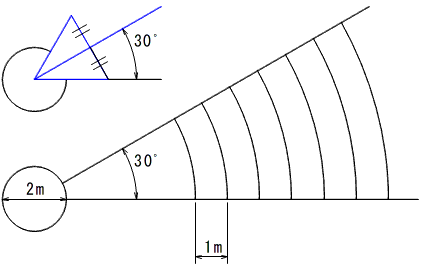文部科学省「新体力テスト」ソフトボール投げの会場は，平坦な地面上に直径２ｍの円を描き，円の中心から投球方向に向かって，中心 角３０°になるように直線を２本引き，その間に同心円弧を１ｍ間隔に 描くようになっています。

中心角３０°は，正三角形の角の二等分線が３０°となることから，巻尺で正三角形とその二等分線を一筆がきして，作成することがあります。このときできる直角三角形の辺の比は，１：２：√３です。

日常生活では，３０°，６０°の角の大きさはあまり見かけませんが，９０°は，生活の中のあらゆるところで使われています。
角の大きさが９０°のところや，２つの直線が垂直に交わるところなどで，３：４：５の辺の比が使えるかもしれません。

②　簡単な整数比でできる角の大きさ

辺の長さの比が，１：１：１の正三角形や３：４：５の直角三角形は，日常で容易に作れます。

その他の簡単な整数比では，どんな大きさの角ができるのでしょうか。参考に調べてみました。
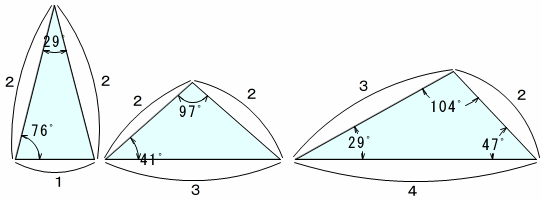・　１：２：２　二等辺三角形で，頂角が約２９°　精度を求めなければ，日常的には，正三角形の二等分線を作るより楽です。
・　２：２：３　二等辺三角形で，頂角約９７°，底角約４１°
・　２：３：４　約１０４°，約４７°，約２９°
・　４：４：１　二等辺三角形で，頂角約１４°，底角約８３°
日常的に使えそうな数の比はこの程度でしょうか。

４　まとめ

３：４：５の比など，三角形の辺の長さの比が，整数比でつくれる角の数が多いと，生活に役立つ場面が増えます。
しかしながら，簡単な辺の長さの比で使えそうな角の大きさをもつ三角形はなかなか無いものです。
三平方の定理については，直角三角形の各辺を一辺とする正三角形や，一辺を直径とする半円でも，同様の関係が成り立つことが分かっています。
このことは演繹的に証明できます。

三角形の辺の長さの比が，３：４：５のときは，斜辺の対角が直角になります。
これは，三平方の定理です。
その他にも，５：１２：１３，７：２４：２５，…などの整数比があります。
辺の長さの比が，１：１：１の正三角形や３：４：５の直角三角形は，日常で容易に作れます。

以上，辺の長さの比に着目して，三角形の辺の長さの比と角の大きさの関係を調べてきました。
これは図形の構成要素に着目した数学的な見方の一つであり，新学習指導要領で示される数学的な見方・考え方です。

【参考】
１：２：２　は，二等辺三角形で，頂角約２９°，底角約７６°
２：２：３　は，二等辺三角形で，頂角約９７°，底角約４１°
２：３：４　は，約１０４°，約４７°，約２９°です。

日常的に使えそうな数の比はこの程度でしょうか。
三角形の辺の長さの比が整数比でつくれる角の数が多いと，生活に役立つ場面が増えます。