- 下のタイルの模様から，ピタゴラスの定理が見えるでしょうか。
図形を調べるときは，どんな見方をするとよいのでしょうか。 
ピタゴラスは，寺院を訪れたとき，床のタイルの模様からピタゴラスの定理を発見したと言われています。
図形を考察する際は，図形の「形」や「量」に着目します。
図形の形，辺や角，頂点という構成要素の特徴や性質，それらの関係，
角の大きさ，長さや面積という量の特徴や性質，それらの関係などです。ピタゴラスの定理の発見を基に，図形の見方を考えます。
１ 図形に対する数学的な見方
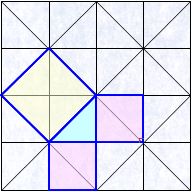
ある寺院に入ったとき，床のタイルの模様が次のようでした。
この模様を数学的な見方で見たとき，どのようなことに気付くでしょうか。
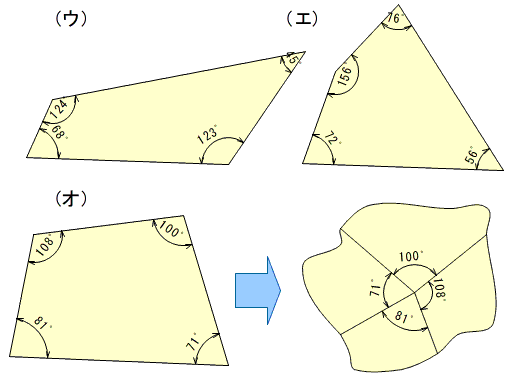
図形の形としては，正方形，長方形，直角二等辺三角形，平行四辺形，菱形の形や性質，またそれらの関係が見られます。
それに伴い，図形の構成要素である辺の長さや角の大きさ，角の和，頂点の個数やそれぞれの関係等が見られます。
さらに，それぞれの図形の面積の関係が見られます。
例えば，次のようなものです。
・ 正方形 は，４つの辺の長さが等しく４つの角がすべて９０度であること，
・ 菱形の対角線は，互いを垂直に２等分すること，
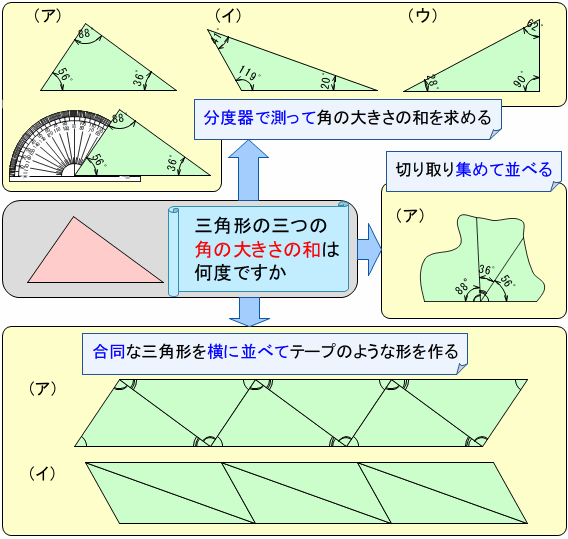
・ 直角二等辺三角形の角の和は１８０度，
・ 正方形は，直角二等辺三角形で構成できること，
・ 面積が直角二等辺三角形の２，４，８個分の正方形が作れること，など。
このように，図形を見るとき，形と量，図形の構成要素やそれらの関係を見ることができます。
２ ピタゴラスの定理の発見
三平方の定理（ピタゴラスの定理）
直角三角形の直角をはさむ２辺の長さをａ，ｂ，斜辺の長さをｃとすると，次の関係が成り立つ。
ａ２＋ｂ２＝ｃ２
ピタゴラスの定理の逆
三角形の三つの辺の長さをａ，ｂ，ｃとするとき，ａ２＋ｂ２＝ｃ２という関係が成り立つならば，この三角形は，ｃという長さの辺に対する角が直角である直角三角形である。
（１）面積の関係の気付き
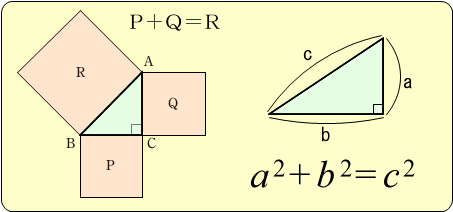
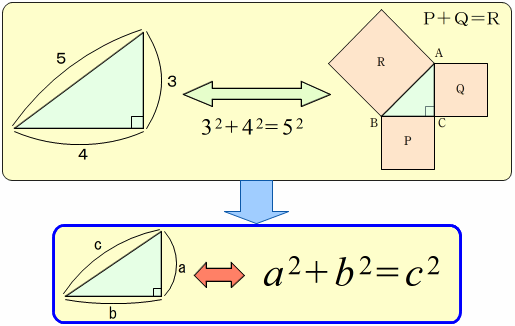
ピタゴラスが，次のような寺院の床のタイル模様を見たとき，三平方の定理を発見したという話が伝えられています。
青色の直角二等辺三角形に着目すると，
直角を挟む２つの辺のそれぞれを一辺とする正方形の面積は，直角二等辺三角形の２つ分（赤色部分）になっています。
一方，直角二等辺三角形の斜辺を一辺とする正方形の面積は，直角二等辺三角形４つ分（黄色部分）になっています。
したがって，赤色の正方形２つ分の面積と，黄色の正方形の面積は，ともに二等辺三角形４個分で等しくなります。
少なくとも，直角二等辺三角形においては，直角を挟む各辺を一辺とする正方形の面積の和と斜辺を一辺とする正方形の面積は，等しいといえます。
このことが，他の直角三角形でも，すなわち一般的に成り立つのかが問題です。
（２）数と図形の関係に着目
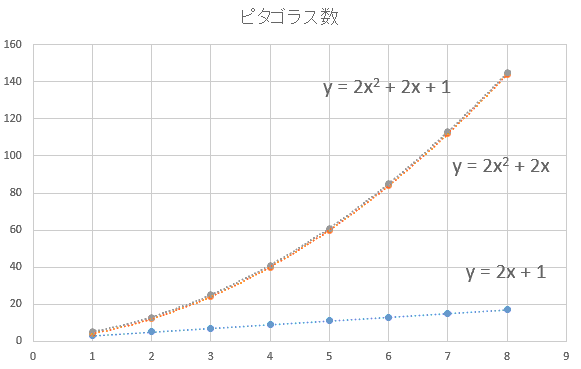
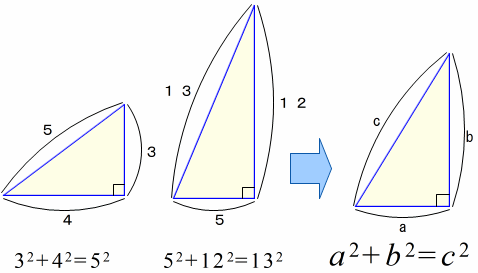
当時，三角形の辺の比が，３：４：５や５：１２：１３が直角三角形になることをピタゴラスが知っていたと考えられています。
これらに加えて，７：２４：２５などの比も含めて，いくつかの特殊な事例は確認できていたらしいのです。
したがって，それらの事例を基に，一般的なａ２＋ｂ２＝ｃ２を帰納したと想像できそうです。
さて，ピタゴラスの定理の証明について，少年アインシュタインが「頂点から対辺へ垂線を引いた証明」を自力で見出しました。
これをきっかけに，１４，１５歳の時には，解析幾何や微積分を独習したというエピソードがあります。
桑木或雄「アインシュタイン伝」偉人伝全集第18巻昭和9インターネット公開（保護期間満了）[ONLINE]http://dl.ndl.go.jp/info:ndljp/pid/1186608/17（cf2017/6/1）
伝記では，その証明方法について言及していませんが，次の証明方法と考えられます。
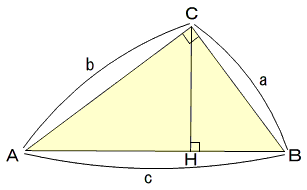ＣからＡＢに下ろした垂線の足をＨとする。
△ＢＨＣ∽△ＢＣＡ なので，
ＢＣ２＝ＢＨ×ＡＢ…①
△ＡＨＣ∽△ＡＣＢ なので，
ＡＣ２＝ＡＨ×ＡＢ…②
①②を辺々加えると
ａ２＋ｂ２＝（ＡＨ＋ＢＨ）ｃ＝ｃ２
ピタゴラスの定理の証明方法は，数百通りあることが知られています。
下の一例や別稿「３：４：５の三角形で，本当に直角ができる？」を参照下さい。
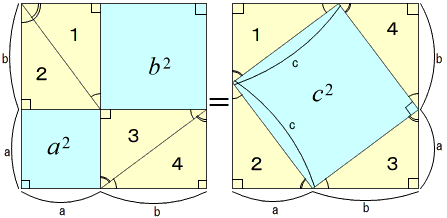
左右の正方形の面積はともに（ａ＋ｂ）２です。黄色１～４の直角三角形が合同であることから，これらを（ａ＋ｂ）２の正方形から取り除くことで，ａ２＋ｂ２＝ｃ２が導かれます。右図のみで同様の説明ができます。
３ まとめ
ピタゴラスが，直角三角形において「辺の長さの比」と「辺の長さに依存する正方形の面積」との関係，数(数式)と図形の関係に着目して定理を見出してることが興味深いところです。
図形を考察する際は，図形の「形」と「量」に着目することが必要です。
前者は，小学校算数科では，図形領域の指導内容，後者は量と測定の指導内容になります。
特に，「量」は測定という数値化を伴うことから，数計算領域の内容を必要とします。
着目する点としては，
・ 図形の形，辺や角，頂点という構成要素の特徴や性質，それらの関係
・ 角の大きさ，長さや面積という量の特徴や性質，それらの関係などです。
ピタゴラスは，図形を，数や数式と関連させている点で，興味深い数学的な見方・考え方を発揮しています。
