- 方べきの定理とは，どういうものでしょう。
- 1つの円と1つの点が与えられ，その点を通る2つの直線と円がつくる線分の積が一定となるものです。
方べきの定理
点 \(A\) を通る任意の直線が円 \(O\) と交わる点を \(P,Q\) とすると \(AP\cdot AQ\) は一定です。
特に，\(A\) が円外のときは，この一定値は，\(A\) からこの円に引いた接線の長さの二乗に等しくなります。
これを方べきの定理といい，この一定値を \(A\) のこの円に関する方べきといいます。
方べき
方べきとは，与えられた点から与えられた円までの相対距離を反映する実数です。
１ 方べき
方べき（power of a point）とは，与えられた点から与えられた円までの相対距離を反映する実数です。
具体的には，半径 \(r\) の円 \(O\) に対する点 \(A\) の方べき \(h\) は，次のように定義されます。
\[\begin{equation}\begin{split}AT^2&=AP\cdot AQ\\&=AR\cdot AS\\&=(s-r)\times (s+r)\\&=s^2-r^2=h\end{split}\end{equation}\]
ここで，\(s\) は点 \(A\) と円の中心 \(O\) の間の距離です。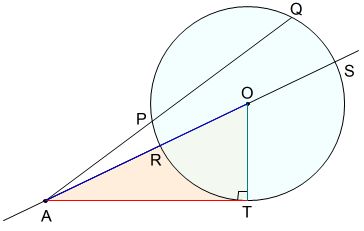
この定義により，円の内側の点は負の方べきをもち，外側の点は正の方べきをもち，円上の点は \(0\) の方べきをもちます。
円 \(O\) の外部に点がある場合，方べきは，点 \(A\) から円 \(O\) への接線の長さの2乗に等しくなります。*1
点 \(A\) を通る任意の直線が円 \(O\) と交わる点を \(P,Q\) とすると \(AP\cdot AQ\) は一定です。
特に，\(A\) が円外のときは，この一定値は，\(A\) からこの円に引いた接線の長さの二乗に等しくなります。
これを方べきの定理といい，この一定値を \(A\) のこの円に関する方べきといいます。*2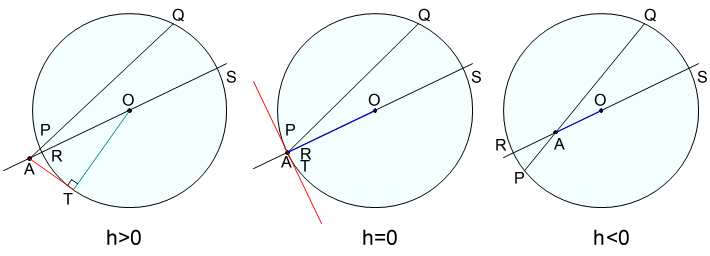
２ 相似を使った証明
（１）二割線の場合
点 \(A\) を通る二つの直線が，円 \(O\) とそれぞれ２点 \(P,Q\) および \(R,S\) で交わっているとき，次の式が成り立つ。*3\[AP\cdot AQ=AR\cdot AS\]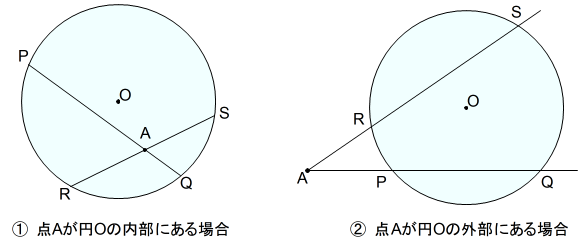
① 点 \(A\) が円 \(O\) の内部にある場合
【証明】
\(△APR\) と \(△ASQ\) において
同じ弧に対する円周角はそれぞれ等しいので
\[∠APR=∠ASQ,∠ARP=∠AQS\tag{1}\]
また，対頂角は等しいので
\[∠PAR=∠SAQ\tag{2}\]
(1),(2)より二つの角が等しいので
\[△APR∽△ASQ\tag{3}\]
(3)より
\[AP:AR=AS:AQ\]
\[\therefore \quad AP\cdot AQ=AR\cdot AS\]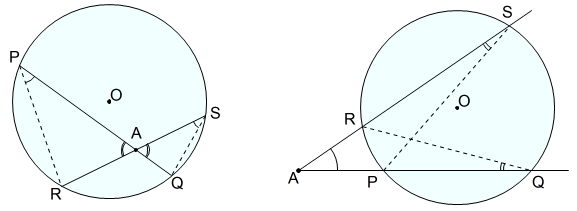
② 点 \(A\) が円 \(O\) の外部にある場合
【証明】
\(△APS\) と \(△ARQ\) において
同じ弧に対する円周角は等しいので
\[∠ASP=∠AQR\tag{1}\]
また，\(∠A\) は共通なので
\[∠PAS=∠RAQ\tag{2}\]
(1),(2)より二つの角が等しいので
\[△APS∽△ARQ\tag{3}\]
(3)より
\[AP:AS=AR:AQ\]
\[\therefore \quad AP\cdot AQ=AR\cdot AS\]
（２）割線と接線の場合
円外の点 \(A\) を通る二つの直線の一方が円 \(O\) と２点 \(P,Q\) で交わり，もう一方が点 \(T\) で接しているとき，次の式が成り立つ。*3\[AT^2=AP\cdot AQ\]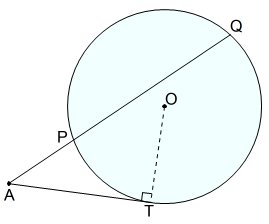
【証明】
\(△APT\) と \(△ATQ\) において
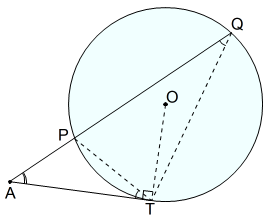
接弦定理より
\[∠PTA=∠TQA\tag{1}\]
また，\(∠A\) は共通なので
\[∠PAT=∠TAQ\tag{2}\]
(1),(2)より
\[△APT∽△ATQ\tag{3}\]
(3)より
\[AP:AT=AT:AQ\]
\[\therefore \quad AP\cdot AQ=AT^2\]
３ 三平方の定理を使った証明
（１）点 \(A\) が円 \(O\) の内部にある場合
点 \(A\) を通る任意の直線が円 \(O\) と交わる点を \(P,Q\) とすると \(AP\cdot AQ\) は一定である。*2
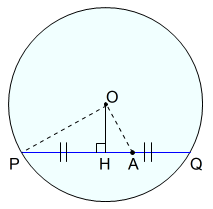方べきの定理を三平方の定理を使って証明します。
円の中心 \(O\) から \(PQ\) への垂線をひき，\(PQ\) と垂線の交点を \(H\) とします。このとき，\(HP=HQ,∠OHP=∠R\) です。
\(∠OHP=∠OHA=∠R\) なので，\(△OHP,△OHA\) は直角三角形です。したがってこれらの三角形においては，三平方の定理が成り立ちます。
\[\begin{equation}\begin{split}AP\cdot AQ&=(HP+AH)(HQ-AH)\\&=(HP+AH)(HP-AH)\\&=HP^2-AH^2\quad \quad \quad \quad (1)\end{split}\end{equation}\]
ここで，\(△AOH\) において，
\[\begin{equation}\begin{split}OH^2+AH^2&=AO^2\\AH^2&=AO^2-OH^2\quad \quad (2)\end{split}\end{equation}\]
また，\(△POH\) において，
\[\begin{equation}\begin{split}OH^2+HP^2&=OP^2\\HP^2&=OP^2-OH^2\quad \quad (3)\end{split}\end{equation}\]
\((1)\)に\((2),(3)\)を代入すると，
\[\begin{equation}\begin{split}AP\cdot AQ&=HP^2-AH^2\\&=OP^2-OH^2-(AO^2-OH^2)\\&=OP^2-OH^2-AO^2+OH^2\\&=OP^2-AO^2\end{split}\end{equation}\]
\(OP\) は円 \(O\) の半径なので 一定です。また，点 \(A\) は定点なので \(AO\) も一定です。したがって \(OP^2-AO^2=AP\cdot AQ\) は一定です。
（２）点 \(A\) が円 \(O\) の外部にある場合
点 \(A\) を通る任意の直線が円 \(O\) と交わる点を \(P,Q\) とすると \(AP\cdot AQ\) は一定である。
特に，\(A\) が円外のときは，この一定値は，\(A\) からこの円に引いた接線の長さの二乗に等しい。
これを方べきの定理といい，この一定値を \(A\) のこの円に関する方べきという。*2
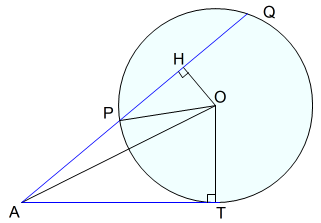
方べきの定理を三平方の定理を使って証明します。
円の中心 \(O\) から \(PQ\) への垂線をひき，\(PQ\) と垂線の交点を \(H\) とします。このとき，\(HP=HQ,∠OHP=∠R\) です。
点 \(A\) から円 \(O\) に引いた接線の接点を点 \(T\) とします。このとき，\(∠ATO=∠R\) です。
\(∠AHO=∠ATO=∠R\) なので，\(△AOH,△PHO,△AOT\) は直角三角形です。したがってこれらの三角形においては，三平方の定理が成り立ちます。
\[\begin{equation}\begin{split}AP\cdot AQ&=(AH-HP)(AH+HQ)\\&=(AH-HP)(AH+HP)\\&=AH^2-HP^2\quad \quad \quad \quad (1)\end{split}\end{equation}\]
ここで，\(△AOH\) において，
\[\begin{equation}\begin{split}OH^2+AH^2&=AO^2\\AH^2&=AO^2-OH^2\quad \quad (2)\end{split}\end{equation}\]
また，\(△POH\) において，
\[\begin{equation}\begin{split}OH^2+HP^2&=OP^2\\HP^2&=OP^2-OH^2\quad \quad (3)\end{split}\end{equation}\]
\((1)\)に\((2),(3)\)を代入すると，
\[\begin{equation}\begin{split}AP\cdot AQ&=AH^2-HP^2\\&=AO^2-OH^2-(OP^2-OH^2)\\&=AO^2-OH^2-OP^2+OH^2\\&=AO^2-OP^2\quad \quad \quad \quad (4)\end{split}\end{equation}\]
\(OP\) は円 \(O\) の半径なので \(OP=OT\)，また，\(△AOT\) は直角三角形なで，三平方の定理より，\(AO^2=AT^2+OT^2\)
これを \((4)\) に代入すると
\[\begin{equation}\begin{split}AP\cdot AQ&=AO^2-PO^2\\&=AT^2+OT^2-OT^2\\&=AT^2\\\therefore \quad AP\cdot AQ&=AT^2\end{split}\end{equation}\]
まとめ
方べき
方べきとは，与えられた点から与えられた円までの相対距離を反映する実数です。
点 \(A\) と円の中心 \(O\) の間の距離を \(s\) とすると，半径 \(r\) の円 \(O\) に対する点 \(A\) の方べき \(h\) は，次のように定義されます。
\[\begin{equation}\begin{split}AT^2&=AP\cdot AQ\\&=AR\cdot AS\\&=(s-r)\times (s+r)\\&=s^2-r^2=h\end{split}\end{equation}\]
方べきの定理
点 \(A\) を通る任意の直線が円 \(O\) と交わる点を \(P,Q\) とすると \(AP\cdot AQ\) は一定です。
特に，\(A\) が円外のときは，この一定値は，\(A\) からこの円に引いた接線の長さの二乗に等しくなります。
これを方べきの定理といい，この一定値を \(A\) のこの円に関する方べきといいます。
証明
方べきの定理の証明は，同じ弧に対する円周角が等しい性質を使って三角形の相似を確かめ，辺の比が等しいことを利用して証明したり，直角三角形を作って共有する辺をもとに長さを置き換え三平方の定理を使って証明したりすることができます。
*1 参考 Wikipedia”Power of a point”[ONLINE]https://en.wikipedia.org/wiki/Power_of_a_point(cf.2020-07-14)
*2 参考 栗田稔 教職数学シリーズ「幾何」共立出版
*3 参考 新興出版啓林館 FocusUp数学IA三訂版
