- 長方形の面積は，「たての長さ」×「横の長さ」で求められると考えてよいのでしょうか。
- 長方形の面積＝たての「数」×横の「数」と考えます。
面積は，図形を敷き詰めた単位正方形のいくつ分かの数で表します。
単位正方形\(E\) の面積を \(1\) とし，図形\(A\) の面積が単位の \(a\) 倍に当たるとき，その数 \(a(a \in \mathbb{ R })\) は図形\(A\) の面積です。
それは図形\(A\) から実数\(a\) への対応であり，面積は，図形から数への関数といえます。
２辺の長さ \(a,b(a,b \in \mathbb{ R })\) の長方形の面積は， \(a \times b\) で求められます。長方形の面積が辺の長さの数値に比例することから，無理数の長さの辺をもつ長方形も，「たて×よこ」で求めてよいことになります。
１ 算数での面積の意味
（１）長方形の面積を求める公式
① 公式の学び方
小学校第４学年で，長方形と正方形の面積の意味と面積を求める公式を学びます。
長方形と正方形の面積は，たてと横の長さがそれぞれ何cmあるかを測り，その数値をかけ合わせて求めることができます。
単位正方形の面積は，１cm2とします。そして，長方形と正方形の面積を求める公式は，
長方形の面積＝たて×横
正方形の面積＝一辺×一辺
と学びます。ところが，2cm×3cm のように，
長方形の面積＝たての「長さ」×横の「長さ」
と考え，面積は「長さ」が集まったものと誤解することがあります。
② 単位の決め方
面積は，広さを単位のいくつ分かで表した数です。その単位はどのように決めるのでしょう。
面積などの量の単位は，比べたい量と同種の量から選ぶ必要があります。
・ 長さなら，長さの単位。例えば，１cmの長さ
・ 体積なら，体積の単位。例えば，１cm3の立方体の体積
長さなら１とする長さ，面積なら１とする面積，体積なら１とする体積です。
このように，面積ならば，同種の量の面積から単位を選びます。
その単位とする図形は，敷き詰めが容易な正方形が便利です。
その理由は，隙間なく埋め尽くせることが必要だからです。正方形なら容易に敷き詰められます。しかも，単位正方形の一辺の長さは，長さの単位と共通する１cmを単位にできるからです。
正方形の一辺の長さを１cmにすれば，長方形等の辺の長さの数値と単位正方形の個数とが数として等しくなります。そのことによって，縦と横の長さを表す数を使って乗法で手際よく乗法で面積が求められるようになります。
③ 公式の意味
長方形の面積を求める公式は，次のようです。
長方形の面積＝たて×横
この公式は何を計算しているかというと，長方形の辺の長さの数値を利用して，中に敷き詰められる単位正方形の数を計算しています。
したがって，
長方形の面積＝たての「長さ」×横の「長さ」
ではなく，
長方形の面積＝たての長さを表す「数」×横の長さを表す「数」
といえます。あくまでも，面積を手際よく求めるために，辺の長さの数値を利用しているだけです。
長方形の面積を求める公式をつくるまでの内容を，小学校ではおおよそ次のように学びます。
（２）１cm2の正方形を使った広さ比べ
「どちらがどれだけ広いですか。」
「１cm2の正方形が，何こ分あるかでくらべましょう。」
【問い】「広さを数で表すしかたを考えよう。」
【問い】「しき石のかわりに，何を単位にするとよいだろう。」
長方形や正方形の面積を測定する単位は，１辺が１cmの正方形が適当であることを理解できるようにします。
単位とする図形の適切な図形
・ 正方形ならば，縦と横の長さが同じであることから，それらを別々に考える必要はなく縦と横の数値を同じように測定・計算できる。
・ 正方形ならば，回転しても（ただし90°単位）構成される図形は変わらないので実際の操作がしやすい。
・ 仮に，単位とする図形を長方形とすると，辺の長さの数値とその辺に並べる単位長方形の個数が等しくならない。そのため余分な計算を要する。また，単位長方形の並べ方についても共通理解を図る必要がある。
・ 単位とする図形を円にすると，隙間ができて面積を正確に測定できない。
単位とする図形の適切な大きさ
・ 正方形の一辺の長さを１cmとし，それを単位とすると，長さの数値と単位正方形の個数とが等しくなり面積の測定が容易になる。
・ 仮に，単位とする正方形の一辺を２cmにすると，辺の長さの数値を２で割る計算が必要となる。
このようにして，
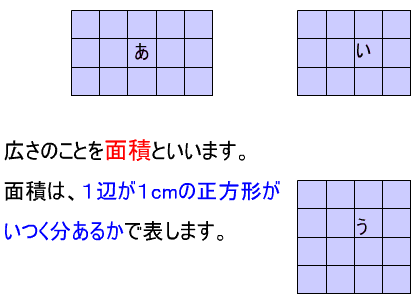
（あ）の長方形の面積＝３×５＝１５ 答え １５cm2 単位正方形が１５個
（い）の長方形の面積＝３×４＝１２ 答え １２cm2 単位正方形が１２個
（う）の長方形の面積＝４×４＝１６ 答え １６cm2 単位正方形が１６個
となります。
（あ）の長方形 → １５
（い）の長方形 → １２
（う）の長方形 → １６
というように，面積を求めると，図形に数を対応させることになります。
２ 面積の数学的な意味
（１）図形から数への関数
面積は広さを単位のいくつ分かで表した数であり，面積を求めることは対象の図形に敷き詰められる単位正方形の数を求めることである，と説明しました。
もう少し数学的に表現すると，面積とは，閉じた図形に数を対応させたものといえます。
つまり，面積は図形から数への対応，図形から数の関数と見ることができます。
関数とは，例えば，「アメリカ合衆国」の首都は，「ワシントン」です。など，一つの要素「国」が，必ず一つの要素「首都」に対応する関係をいいます。閉じた平面図形を描けば，必ず対応する「数」があるようにします。
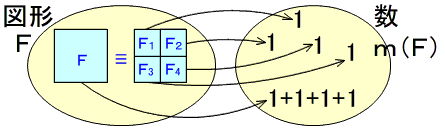
図形の集合があって，その要素をＦ，負でない数を対応させる像をｍ（Ｆ）とします。
このｍ（Ｆ）が面積です。
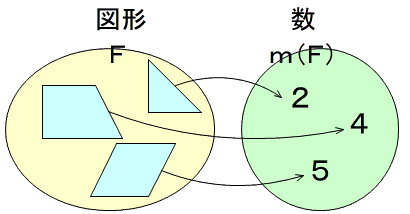
例えば，上図では，図形の集合Fに，三角形，台形，平行四辺形があります。
この一つ一つに，
・ 求積（三 角 形）＝２
・ 求積（台 形）＝４
・ 求積（平行四辺形）＝５
と，単位正方形の数２，４，５が対応します。
（２）満たすべき法則
図形の集合があって，その要素を \(F\)，負でない数を対応させる像を \(m(F)\) とします。
これが次の法則に従っているとします。
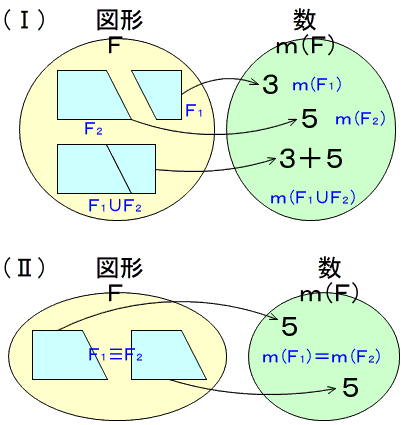
（Ⅰ）２つの図形 \(F_1\) と \(F_2\) に重なりがないとき，\(F_1\) と \(F_2\) をあわせたもの \(F_1 \cup F_2\) の面積は，それぞれの数の和であるようにする。
$$\begin{equation}\begin{split}&F_1 \cap F_2=φ \rightarrow\\&m(F_1 \cup F_2)=m(F_1)+m(F_2)\end{split}\end{equation}$$
（Ⅱ）\(F_1\) と\(F_2\) が合同のときは，対応する数は等しくする。
$$F_1 \equiv F_2 \rightarrow m(F_1)=m(F_2)$$
さらに，\(E\) を単位図形とすると，\(m(E)=1\)，線分の面積は，\(0\) です。
ある図形を単位図形 \(E\) の和に分割します。そうすると面積はそれに対応する数の和になります。
（３）面積の求め方
$$\begin{equation}\begin{split}m(F)&=m(F \cup φ)\\&=m(F)+m(φ)\\&=m(F)\end{split}\end{equation}$$
（Ⅰ）から$$m(φ)=0$$
これは，例えば，三角形に線分を付け加えても，線分の面積は \(0\) なので，三角形の面積は変わらない。
線分の面積は，\(0\) ですという意味です。
数学的にいうと，図形が空集合のときは，数は \(0\) が対応します。
すなわち面積は \(0\) です。
$$\begin{equation}\begin{split}&F_1 \cap F_2=φ →\\&m(F_1 \cup F_2)=m(F_1)+m(F_2)-(F_1\cap F_2)\end{split}\end{equation}$$
\(F_1\) と \(F_2\) に重なりのある場合は，重なった部分の図形に対応する数である重複部分の面積をひきます。
要するに，「（２）満たすべき法則」の意味は，
・ 合同のときには，同じ数を対応させる
・ 図形の和，重なりのない和ならば，それに対応する数も和とする
この２つを満足するように，図形に数を対応させたものが面積です。
記号でかくと以下のようになります。
$$\begin{equation}\begin{split}&F \equiv F_1 \cup F_2 \cup F_3 \cup \cdots \cup F_n,\\&\quad \quad F_i \cap F_j=φ →\\&m(F)=m(F_1)+m(F_2)+m(F_3)+…\\&\quad \quad \quad \quad +m(F_n)\end{split}\end{equation}$$…（ア）
$$F_1 \subseteq F_2 → m(F_1) \leqq m(F2)$$…（イ）
（ア）の式の具体例を考えます。
\(F_n\) を単位図形 \(E_n\) とします。
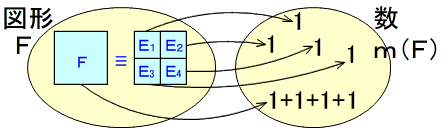
図形 \(F\) を，単位図形 \(E\) で重なりのないように敷き詰め，\(E_n\) の和に分割できたとします。
そうすると，図形 \(F\) は，\(E_1 \cup E_2 \cup E_3 \cup E_4\) と合同になります。
合同な図形は対応する数が等しことから，
面積 \(m(F)\) は，それに対応する数の和 \(m(E_1)+m(E_2)+m(E_3)+m(F_4)\) と等しいことになります。
ここで，\(m(E_n)=1\) なので，
$$m(F)=1+1+1+1=4$$
となり，図形 \(F\) の面積 \(m(F)\) は \(4\) となります。
このことは，外延量である面積が，量の保存性と加法性をもつことを示しています。
・ 量の保存性…ものの形を変形したり，幾つかに分割したり，位置を動かしたりしても，そのものの量の大きさは変わらない。
・ 量の加法性…測定したい２つのものを合併したときの量が，それぞれのものの量の加法によって計算できる。
３ 無理数でも成り立つ公式
【定理１】２辺の長さ \(a,b\) の長方形の面積は \(ab\) である。*1
証明 \(a,b\) が自然数，分数，無理数の場合を分けて順に証明します。
\(a,b\) が自然数のとき
\(a,b\) が自然数のときは，それぞれの辺を \(a\) 等分，\(b\) 等分する点を通って辺に平行な直線を引いて１辺の長さが \(1\) の正方形の \(ab\) 個に分割すると，（Ⅰ）によって長方形の面積は，\(ab\) となる。
\(a,b\) が分数のとき
\(a,b\) の少なくとも一方が分数のときは，
$$a= \dfrac{q}{p},b= \dfrac{s}{r} (p,q,r,s \in \mathbb{ N })$$
とおいてそれぞれの辺を \(p\) 倍，\(r\) 倍に伸ばして辺の長さ \(q,s\) の長方形をつくると，（１）によってその面積は，\(qs\) である。
もとの長方形の面積を \(S\) とすると，上で作った長方形の面積 \(S\) の長方形を \(pr\) 個集めたものだから（１）によって
$$prS=qs$$
$$∴ S=\dfrac{qs}{pr}=\dfrac{q}{p} \cdot \dfrac{s}{r}=ab$$
\(a,b\) が無理数のとき
\(a,b\) の少なくとも一方が無理数のときは，\(a\) は有理数の列 \(x_1 \lt x_2 \lt x_3 \lt …\) と \(y_1 \gt y_2\gt y_3\gt …\) をとって
$$a=\displaystyle \lim_{ n \to \infty } x_n,a=\displaystyle \lim_{ n \to \infty } y_n$$
とすることができる。
また，\(b\) も有理数の列 \(u_1 \lt u_2 \lt u_3 \lt …\) と \(v_1 \gt v_2\gt v_3\gt …\) をとって
$$b=\displaystyle \lim_{ n \to \infty } u_n,b=\displaystyle \lim_{ n \to \infty } v_n$$
とすることができる。
ここで，はじめの長方形（面積を \(S\) とする）は，２辺の長さ \(x_n,u_n\) の長方形を含み，２辺の長さ \(y_n,v_n\) の長方形にふくまれるから（２）と（イ）によって
$$x_nu_n \leqq S \leqq y_nv_n$$
そこで，\(n \to \infty\) とすると，
$$ab \leqq S \leqq ab$$
となって，$$S=ab$$
４ 無理数の辺の長さは数の拡張
（１）無理数の辺は，有理数の単位正方形で埋め尽せない
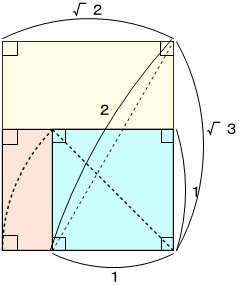長さを表す数が有理数の場合は，共通な単位分数が必ず存在します。だから，その単位分数を考えれば，長方形の面積は，かけ算で求めることができます。
ところが，無理数の場合は，共通する単位が存在しないので，有理数のように整数に直して考えることができません。
したがって，無理数の長さの辺をもつ長方形や正方形を，有理数の正方形で埋め尽くすことはできません。
縦の長さが \(\sqrt{ 3 }\) ，横の長さが \(\sqrt{ 2 }\) の長方形は，実際に作図できるので面積は存在するはずですが，有理数の範囲では正確に測定できないことになります。それでは困ります。
そこで，数の拡張を考えます。
（２）数の拡張
縦が２cmの長方形の面積について考えることにします。
その長方形の横の長さが１cmのとき面積は２×１となり２cm2です。
横が２cmになると，面積は２×２，
横が３cmになると，面積は２×３，
で求められます。長方形の面積は横の長さに比例するので，
横が１に当たる大きさは，２×１で２，
横が２に当たる大きさは，２×２で４ ，
横が３に当たる大きさは，２×３で６，
と表現できます。横の長さの数値が小数でも同様です。
横が2.3に当たる大きさは，２×2.3で4.6，
と表現できます。
横の長さが\(\sqrt{ 2 }\) の場合も同様です。横が\(\sqrt{ 2 }\) に当たる大きさは，\(2 \times \sqrt{ 2 }\) で \(2\sqrt{ 2 }\)
実数の連続性から，無理数に当たる直線の長さが存在し，無理数の辺の長さをもつ長方形が存在します。長方形の面積は横の長さに比例することから，辺の長さが無理数のときも，長方形の面積は縦×横で求めてよいことになります。
面積は横の長さの数値に比例することと実数の連続性から，辺の長さが無理数であってもかけ算で求められます。すなわち \(S=ab(a,b \in \mathbb{ R })\) です。
【ポイント】
〇 面積は，図形から数への対応，図形から数への関数です。
$$\begin{equation}\begin{split}&F \equiv F_1 \cup F_2 \cup F_3 \cup … \cup F_n,\\&\quad \quad F_i \cap F_j=φ →\\&m(F)=m(F_1)+m(F_2)+m(F_3)+…\\&\quad \quad \quad \quad +m(F_n)\end{split}\end{equation}$$
〇 ２辺の長さ\(a,b(a,b \in \mathbb{ R })\) の長方形の面積は \(a \times b\) です。
〇 長方形の面積が辺の長さの数値と比例関係にあることをもとに考えると，無理数の辺の長さでも「たて×よこ」として，長方形の面積が求められることを理解できます。
例えば，長方形の縦の長さを \(2cm\) に固定して横の長さを変えるとき，横の長さが \(1cm\) のときは面積が \(2 \times 1=2(cm^2)\)， \(\sqrt{ 2 }cm\) のときは \(2 \times \sqrt{ 2 }=2\sqrt{ 2 }(cm^2)\) とでき，面積は \(\sqrt{ 2 }\) 倍になります。面積は横の長さの数に比例します。
＊１ 引用文献 栗田稔「教職数学シリーズ基礎編２幾何」共立出版１９８１年
