- 三平方の定理に登場する 3:4:5 などの辺の比は,どのようにつくるのでしょうか。
- まず,次の式を見てください。
1+3+5=32
1+3+5+7=42
1+3+5+7+9=52なんとも不思議です。
奇数の和が,平方数になっています。
この3つの式を組み合わせると,32+42=52
正の整数a,b,cがa2+b2=c2の関係を満足していれば,a,b,cの組をピタゴラス数と呼びます。
ピタゴラス数は,奇数の和である平方数をもとに構成できます。
例えば,よく知られる(3,4,5)は,次のように導かれます。1+3+5+7=42………①
1+3+5+7+9=52…②
①を②に代入すると,
42+9=52
42+32=52この方法で一般的な求め方は,自然数nを用いて,
a=2n+1,b=2n2+2n,c=2n2+2n+1
となります。
より一般的な方法は,異なる自然数m,nを用いて次のように表されます。a=m2-n2,b=2mn,c=m2+n2
1 奇数の和は平方数
(1)ピタゴラス数とは
有名なピタゴラスの定理は,次のように述べることができます。
直角三角形において,直角をはさむ二辺の上にかいた正方形の面積の和は,その斜辺の上にかいた正方形の面積に等しい。すなわち,直角三角形の直角をはさむ二辺の長さをそれぞれa,b,斜辺の長さをcとすれば,
a2+b2=c2
が成り立つ。
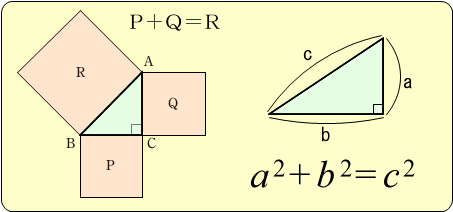
ピタゴラスの定理は,その逆も成り立ちます。
三角形の三つの辺の長さをa,b,cとするとき,もしその間に,
a2+b2=c2
という関係が成り立つならば,
この三角形は,cという長さの辺に対する角が直角である直角三角形である。
このことから,ピタゴラスの定理が成り立つ数の組を,ピタゴラス数と呼んでいます。
正の整数a,b,cがa2+b2=c2の関係を満足していれば,a,b,cの組はピタゴラス数
例えば,
32+42=52
(3,4,5)は,比較的よく知られたピタゴラス数です。
日常的に,直角を作ったり確かめたりするときに使われます。
(2)奇数の和と平方数の関係
ところで,自然数で,1,3,5,7,9,…,2n-1は,奇数です。
その奇数を,1から順に加えていくと,次のようになります。
1=12
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
1+3+5+7+9+11=36=62
……
不思議なことに,奇数の和は,平方数になります。
平方数とは,自然数の二乗で表される整数です。
ピタゴラスは,この平方数のことを四角数と呼びました。
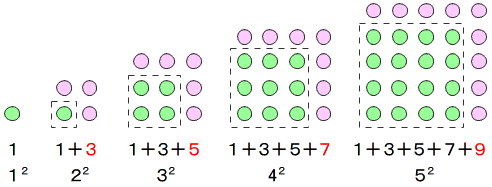 図のように,
図のように,
- n個×n個の正方形を作ります。
- その正方形の上に,辺の数と同じn個を加え,
- 正方形の右に,辺の数と同じn個を加え,
- 正方形の右上に,1個を加えます。
- 合わせて,2n+1,すなわち奇数個を加えたことなります。
- そうすると,できた正方形は,(n+1)個×(n+1)個の正方形です。
はじめのn個×n個の正方形から,(n+1)個×(n+1)個の正方形に変わり,(n+1)2の平方数になります。
このように,連続する奇数を加えることで,平方数を続けてつくることができます。
奇数を,1から順に加えた結果は,いつでも平方数になります。
1+3+5+7+…(2n-1)=n2
2 平方数から構成するピタゴラス数
ピタゴラスは,奇数の和である平方数をもとに,ピタゴラス数を見出しました。
例えば,以下のようです。
1~7と1~9の奇数の和を考えます。
1+3+5+7=42………①
1+3+5+7+9=52…②
①を②に代入すると,
42+9=52
42+32=52
これにより,ピタゴラス数(3,4,5)が得られます。
次に,1~23と1~25の奇数の和を考えます。
1+3+5+…+23=122………①
1+3+5+…+23+25=132…②
①を②に代入すると,
122+25=132
122+52=132
これにより,ピタゴラス数(5,12,13)が得られます。
さらに,1~47と1~49の奇数の和を考えます。
1+3+5+…+47=242………①
1+3+5+…+47+49=252…②
①を②に代入すると,
242+49=252
242+72=252
これにより,ピタゴラス数(7,24,25)が得られます。
この方法を続ければ,いくらでもピタゴラス数をつくり出すことできます。
例えば,(40,9,41),(60,11,61),(84,13,85)などです。
・ 402+92=412
・ 602+112=612
・ 842+132=852
・ 1122+152=1132
・ 1442+172=1452
3 ピタゴラス数の分析と求め方
(1)ピタゴラス数の作り方を図で考える
上記のピタゴラス数の作り方を図にして考えると,赤文字部分が平方数になるとき,ピタゴラス数になります。
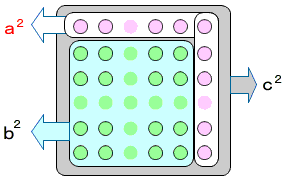
- 一辺がn個であるn個×n個の正方形を作ります。
- その正方形の上に,辺の数と同じn個を加え,
- 正方形の右に,辺の数と同じn個を加え,
- 正方形の右上に,1個を加えます。
- 合わせて,2n+1個を加えます。
- そうすると,できた正方形は,(n+1)個×(n+1)個の正方形です。
このとき,
はじめのn個×n個の正方形は,n2個,最後にできた正方形は,(n+1)個×(n+1)個の正方形,すなわち(n+1)2個の正方形です。
このことを式に表すと,
n2+(2n+1)=(n+1)2
となります。
この(2n+1)が平方数のとき,ピタゴラス数になります。
例えば,奇数は,1,3,5,7,9,11,…
と続きます。
そのうち最初の奇数の平方数は,9=32です。
次の平方数としては,16=42がありますが,これは偶数です。
ですから,さらに次の奇数の平方数を探します。
…,19,21,23,25,27,…
となり,平方数25=52が登場します。
この平方数からピタゴラス数を作ると,
1+3+5+…+23=122………①
1+3+5+…+23+25=132…②
①を②に代入すると,
122+25=132
122+52=132
これにより,ピタゴラス数(5,12,13)が得られます。
(2)ピタゴラス数を式で考える
① ピタゴラス数の図化
上記で得られたピタゴラス数で,直角三角形を作図するとどのようになるでしょうか。
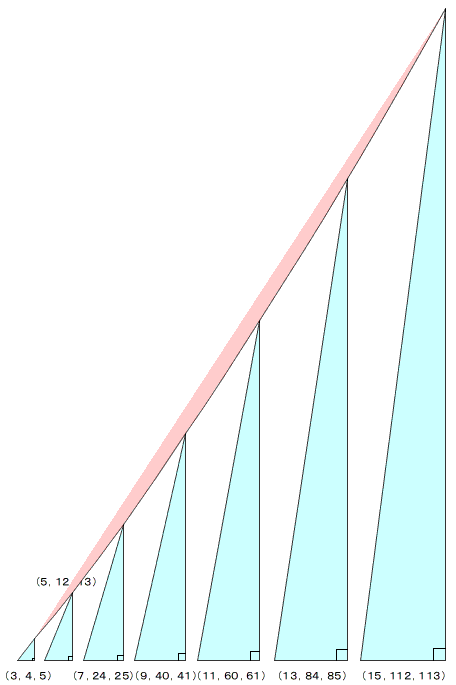
直角を挟む2辺のうち 一方の辺の比は,
3,5,7,9,11,13,15,…
という奇数で,一次的な単調増加です。
他方の辺の比は,
4,12,24,40,60,84,112,…
と,数は二次的に変化し単調増加です。
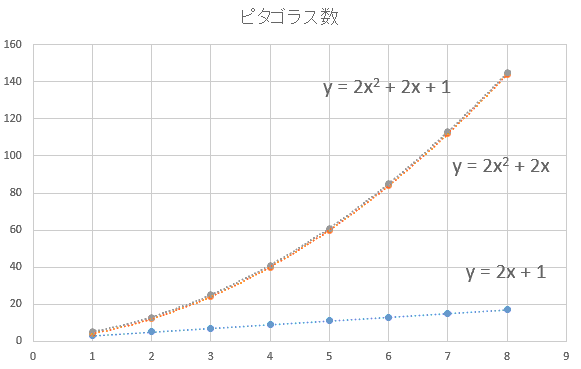
② ピタゴラス数のグラフ化
下記のピタゴラス数である3辺の比の変化を,グラフ化すると次のようになります。
番号( a, b, c ) a2+b2=c2
1 ( 3 4 5)
2 ( 5 12 13)
3 ( 7 24 25)
4 ( 9 40 41)
5 ( 11 60 61)
6 ( 13 84 85)
7 ( 15 112 113)
8 ( 17 144 145)

③ ピタゴラス数の式化
直角三角形の直角をはさむ2辺のうちの1辺の変化の式は,
y=2x+1
の一次関数です。これは,奇数を表します。
直角をはさむもう1辺の変化の式は,
y=2x2+2x
の定数項のない二次関数です。
斜辺の変化の式は,
y=2x2+2x+1
の二次関数です。
「2 平方数からできるピタゴラス数」で述べた方法によれば,一般的に次の式でピタゴラス数が求められます。
自然数:n a:2n+1,b:2n2+2n,c:2n2+2n+1
なお,
a2+b2=(2n+1)2+(2n2+2n)2
=4n4+8n3+8n2+4n+1
=(2n2+2n+1)2
=c2
となり,上記の式は,三平方の定理が成り立ちます。
これらの式のnに自然数を代入すると,ピタゴラス数が得られます。
④ ピタゴラス数の一般的な求め方
さらに一般的には,ピタゴラス数は,次のように表されることが知られています。
| 最大公約数が1のピタゴラス数は,異なる自然数m,nを用いて次のように表される。
x=m2-n2,y=2mn,z=m2+n2 |
4 まとめ
ピタゴラス数は,奇数の和である平方数をもとに構成することができます。
例えば,よく知られる(3,4,5)は,次のように導かれます。
1+3+5+7=42………①
1+3+5+7+9=52…②
①を②に代入すると,
42+9=52
42+32=52
この方法で一般的な求め方は,
自然数:n a=2n+1,b=2n2+2n,c=2n2+2n+1
となります。
より一般的な方法は,異なる自然数m,nを用いて次のように表されます。
a=m2-n2,b=2mn,c=m2+n2
引用,参考文献 矢野健太郎「すばらしき数学者たち」新潮文庫昭和55年(本稿1,2)※平方数は,本書では,三角数と合わせて四角数と紹介されています。本稿では,三角数に触れていないことから,平方数を使用しています。