小学校算数科数学的な考え方「帰納的な考え方」

小学校算数科で育成する数学的な考え方の「帰納的な考え方」とは，どのような考え方なのでしょうか。

いくつかの具体的な例に共通する一般的な事柄を見いだす考え方です。
1.　いくつかのデータを集めようと努める。
2.　それらのデータの間に共通にみられるルールや性質を見出そうと努める。
3.　見いだしたルールや性質が，そのデータを含む集合（変数の変域全体）で成り立つであろうと推測する。
4.　この推測した一般性が真であることをより確かにするために，新しいデータで確かめてみる。
ルールや性質の推測は，推測を調べたり，推測しながら調べたりするなど，順がかわることもあります。








１　はじめに

小学校算数科で学ぶ数学的な考え方として重要なものの一つが帰納的な考え方です。

帰納的な考え方（簡易な説明）
「いくつかの具体的な例に共通する一般的な事柄を見いだす」考え方

帰納的な考え方は，問題解決の見通しをもつ場面や根拠となる事柄を示す場面で用いることが多い考え方です。
なお，学習指導要領解説^*2では「帰納的な考え」ですが，筆者は「帰納的な考え方」としています。
「考え」 は考えた内容や結論をいい，「考え方」 は考える方法や思考の順序をいいます。したがって，帰納的な考え方は，考える方法であることから，「考え方」と表記します。
数学的な考え方の数学的な意味は，片桐重男著「数学的考え方の具体化と指導」^*1によります。
簡便な説明では，「文部科学省小学校学習指導要領解説　算数編」^*2で解説のある場合はその表記によります。

※１９８８年出版の前著「数学的考え方の具体化」片桐重男著は，理論的な解説が充実し，筆者が信頼を寄せる名著です。絶版だったのですが，読みやすく編集され，新版が出版されました。専門的に学びたい方には座右の書にしたい著書の一つです。「帰納的な考え方」の意味については，新版では「努める」が挿入されています。「考え『方』」の意味合いが明確にされ，筆者は大いに賛同します。

２　帰納的な考え方と評価

帰納的な考え方
1. 　いくつかのデータを集めようと努める。
2.　それらのデータの間に共通にみられるルールや性質を見出そうと努める。
3.　見いだしたルールや性質が，そのデータを含む集合（変数の変域全体）で成り立つであろうと推測する。
4.　この推測した一般性が真であることをより確かにするために，新しいデータで確かめてみる。

人が考えている状況を直接捉えて評価することは困難です。そこで，思考の結果として現れるものをもって評価する必要があります。以下では，説明に使用する言葉等を中心にして，帰納的な考え方をしているのかどうかを評価します。
また，帰納的な考え方では，上記の手順を踏んだ思考が必要です。
以下に示す「集める」「見つける」「推測する」「確かめる」は，その考えに基づいた学習活動です。
【集める】いくつかの例を集める
【見つける】それらの例の間に共通にみられるきまりや性質を見つける
【推測する】そのきまりや性質が，その例を含む集まり全体で成り立つだろうと推測する
【確かめる】いつでも成り立つと推測したことを，より確かにするために，新しい例で確かめる

３　事例１　３の段の乗法九九の構成

発展的に考える

◯　続くかける数にも決まりが使えないか考える（類推的・発展的な考え方）
この子どもの気付きを，「九九を広げる」学習に生かすようにします。

３×１０
３×１１
３×１２　も同じようにできるのでは。

◯　他のだんにも決まりが使えないか考える（類推的・発展的な考え方）
この子どもの気付きを，既習の九九の構成の仕方を統合的にとらえられるようにしたり，続く九九の構成に生かすことができるようにしたりします。

２のだんは，「かける数が１ふえると答えは２ずつふえる」のでは（ふえた（既習））
４のだんは，「かける数が１ふえると答えは４ずつふえる」のでは

４　事例２　乗法九九の表

【問題】「九九の答えがどのように並んでいるか，調べましょう」

集める・見つける

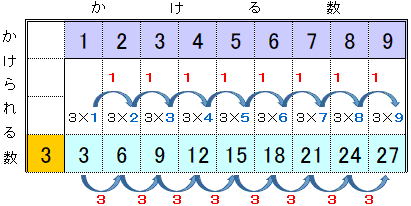Ｃ：「３のだんでは，かける数が１ふえると答えは３だけふえます。」
Ｃ：「４のだんでは，かける数が１ふえると，答えは４ふえると思います。」
Ｔ：「ほかのだんも調べてみましょう。」

Ｃ：「３のだんでは，かける数が１ふえると答えは３だけふえていました。」
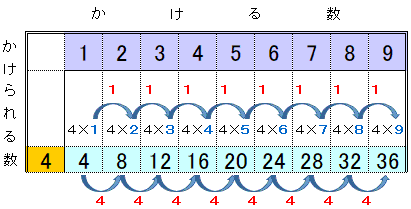Ｃ：「調べると，４のだんでは，かける数が１ふえると答えは４だけふえます。」

推測する

Ｃ：「かけ算では，かける数が１ふえると答えはかけられる数だけふえるのではないかな。」
Ｃ：「７のだんなら，７だけふえるはずです。」

確かめる

Ｃ：「７のだんでも，かける数が１ふえると答えは７だけふえるか確かめてみよう。」
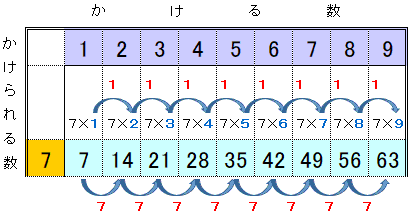Ｃ：「７のだんでも，かける数が１ふえると答えは７だけふえます。」

【まとめ】「かけ算では，かける数が１ふえると答えはかけられる数だけふえる」

５　事例３　四角形の内角の和

【問題】「四角形の４つの角の大きさの和について調べましょう。」

集める

いくつかの例「四角形の4つの角の和」を集めます

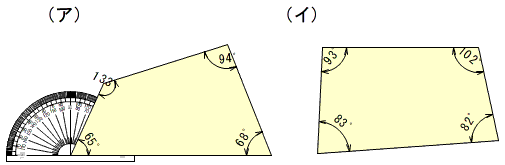
（ア）１３３°＋６５°＋６８°＋９４°＝３６０°
（イ）９３°＋８３°＋８２°＋１０２°＝３６０°

見つける

それらの例の間に共通にみられるきまりや性質を見つけます

（ア）１３３°＋６５°＋６８°＋９４°＝３６０°
（イ）９３°＋８３°＋８２°＋１０２°＝３６０°

アとイの四角形の４つの角の大きさの和は，どちらも３６０°になっています。

推測する

そのきまりや性質が，その例を含む集まり全体で成り立つだろうと推測します
「四角形の４つの角の大きさの和はどちらも３６０°になっているのではないか。」
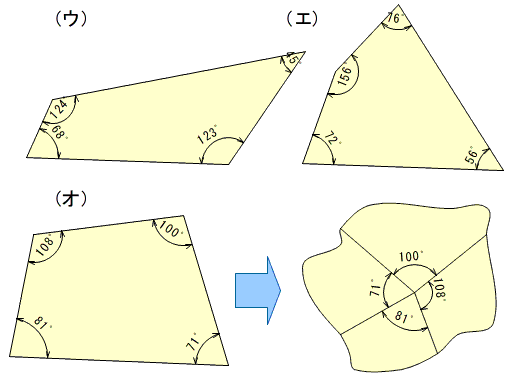
◯　ウとエも３６０°ではないか。
◯　３６０°なら，四角形の４つの角を切り取って１つの点に集めたら，一周の３６０°になるのではないか。

確かめる

いつでも成り立つと推測したことを，より確かにするために，新しい例で確かめます
（ウ）９３°＋８３°＋８２°＋１０２°＝３６０°
（エ）９３°＋８３°＋８２°＋１０２°＝３６０°
四角形（オ）の４つの角を切り取って１つの点に集めたら，敷き詰められて一周の３６０°になります。

【注意】「四角形の４つの角の大きさの和は３６０°」であることをはっきりと説明するためには，四角形を三角形に分け三角形の内角の和が180°であることを根拠とし説明するなど，演繹的に説明する必要があります。

６　まとめ

小学校算数科で育成する数学的な考え方の「帰納的な考え方」は，いくつかの具体的な例に共通する一般的な事柄を見いだす考え方です。詳しくは，次のような思考の流れをする考え方です。

1.　いくつかのデータを集めようと努める。
2.　それらのデータの間に共通にみられるルールや性質を見出そうと努める。
3.　見いだしたルールや性質が，そのデータを含む集合（変数の変域全体）で成り立つであろうと推測する。
4.　この推測した一般性が真であることをより確かにするために，新しいデータで確かめてみる。

ルールや性質の推測は，推測を調べたり，推測しながら調べたりするなど，必ずしも順序性があるわけではありません。

＊１　引用文献　片桐重男　数学的な考え方とその指導第１巻「数学的な考え方の具現化と指導」明治図書２００４年
＊２　参考文献
文部科学省小学校学習指導要領解説算数（1）第1章～第2章（平成20年6月）[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2009/06/16/1234931_004_1.pdf（参照2017/05/16）
文部科学省小学校学習指導要領解説算数（2）第3章～第4章（平成20年6月）[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2009/06/16/1234931_004_2.pdf（参照2017/05/16）
＊３　啓林館　わくわく算数２下平成２７年度版
＊４　参考文献　片桐重男　数学的な考え方・態度とその指導１「数学的な考え方の具現化」明治図書１９８８年