- 小学校算数科で育成する数学的な考え方の「類推的な考え方」とは，どのような考え方なのでしょうか。
- 既習の内容との類似性に着目して新しい事柄を見いだす考え方です。
ある事柄Ａについて，その性質，法則または解決の方法を知りたい。しかし，それがわからないというとき，Ａと似よりの既知の事柄Ａ’を思い出し，（Ａ’については性質や法則，解決の方法などＰ’が分かっているとする），ＡについてもＡ’のＰ’と同様なことが言えるのでないかというように思考を進めていこうと努めるものである
類推的な考え方は，見通しをもったり，根拠を説明したりするときに用いられます。
特に，解決の方法と結果の見通しをもつときに，しばしば活用されます。
１ はじめに
小学校算数科で学ぶ数学的な考え方として，重要でしばしば用いられる考え方が類推的な考え方です。
類推的な考え方（簡易な説明）
「既習の内容との類似性に着目して新しい事柄を見いだす」考え方
問題を解決するため，新しい方法をつくり結果を得ようとするとき，見通しをもち筋道を立てて考えることが必要になります。
見通しをもつには，帰納的な考え方や類推的な考え方を用いることがあります。
・ 見通し：「解決のための方法」についての見通しと「結果」についての見通し
・ 帰納的な考え：いくつかの具体例を調べて共通性を見付ける考え方
・ 類推的な考え：既習の内容との類似性に着目して新しい事柄を見いだす考え方
見通しをもつことは，問題の解決を適切にまた合理的に進めていく上で重要です。
問題解決の方法や結果が正しいことをきちんと示すためには，筋道を立てて考えることが求められます。
・ 筋道を立てて考える：根拠を明らかにしながら，一歩ずつ進めて考えていくこと
・ 演繹的な考え方：ある前提を基にして説明していく考え方。「筋道を立てて考える」代表的な考え方
・ 帰納的・類推的な考え方：根拠となる事柄を示すという点で，筋道を立てた考えの一つ
類推的な考え方は，問題解決の見通しをもつ場面や根拠となる事柄を示す場面で用いることが多い考え方です。
なお，学習指導要領解説*2では「類推的な考え」と表記されていますが，筆者は「類推的な考え方」と表記しています。
「考え」 は考えた内容や結論をいい，「考え方」 は考える方法や思考の順序をいいます。したがって，類推的な考え方は，考える方法であることから，「考え方」と表記します。
数学的な考え方の数学的な意味は，片桐重男著「数学的考え方の具体化と指導」*1によります。
簡便な説明では，「文部科学省小学校学習指導要領解説 算数編」*2で解説されている表記によります。
「類推的な考え方」の意味については，新版では類推の対象を「性質，法則または解決の方法」とし「解決の方法」が挿入されています。見通しをもつことに対応した挿入であり，見通しに正対した類推的な考え方の意味が明確になりました。
※１９８８年出版の前著「数学的考え方の具体化」片桐重男著は，理論的な解説が充実し，筆者が信頼を寄せる名著です。絶版だったのですが，読みやすく編集され，新版が出版されました。専門的に学びたい方には座右の書にしたい著書の一つです。
２ 類推的な考え方と評価
類推的な考え方
ある事柄Ａについて，その性質または法則を知りたい，しかしそれがわからないというとき，Ａと似よりの既知の事柄Ａ’を思い出し（Ａ’については性質または法則Ｐ’が成り立っているとする），そこでＡについてもＰ’と同様な性質またはルールＰが成り立つのではないか，というように思考を進めていこうとするものである。
人が考えている状況を直接捉えて評価することは困難です。そこで，思考の結果として現れるものをもって評価する必要があります。以下では，説明に使用する言葉等を中心にして，類推的な考え方をしているのかどうかを評価します。
また，類推的な考え方では，当面の問題場面と類似した既習の内容，すなわち既知の事項を基に説明します。そのため，基にする既知の事項を明確にする必要があります。
以下に示す「既知の事項」とは，類推的な考え方で説明するときに基にする，当面の問題場面と類似した既に分かっていること，正しいことが明らかになっていることのことです。
３ 事例１ 方法を類推する
三角形の３つの角の大きさの和を求める問題の解決に使った方法を思い出して，同じ方法が使えないかと考ええるのは類推的な考え方です。
まず，四角形の四つの角の大きさの和を考えるときに，類似した既習の問題の解決方法を思い起こします。
類似の解決した問題として，問題の構造が類似した「三角形の３つの角の大きさの和を求める」問題を振り返ります。
方法の見通しをもつ：解決の方法を類推する
【問題】「四角形の４つの角の大きさの和について調べましょう。」この問題と類似した既習の問題を思い出す
既知の事項
「三角形の３つの角の大きさの和について調べましょう。」
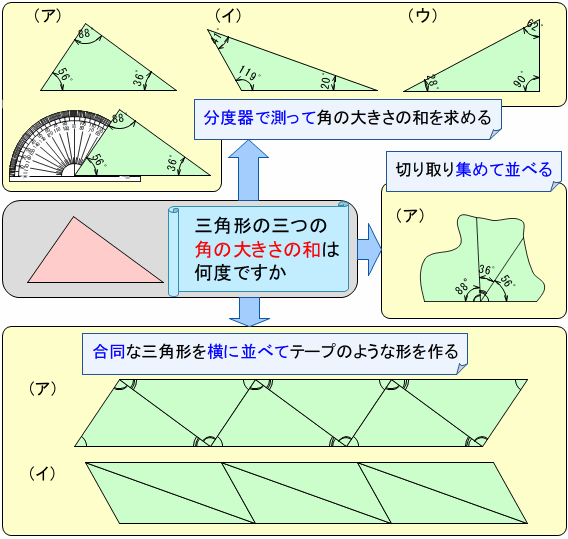
三角形の３つの角の大きさの和を求めるときには，合同な図形を並べたり敷き詰めたりする，分度器で測る，角を切り取り集めて並べる（寄せ集める）方法で調べ，３６０°であることを確かめています。
類推的な考え方
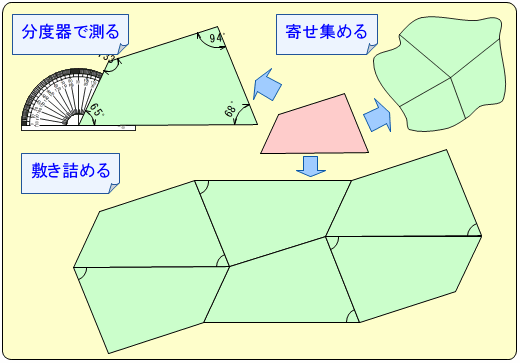
四角形の４つの角の大きさを調べる問題に，三角形の調べ方を当てはめて解決方法を考えると次のようになります。
1. 合同な四角形を（横に並べて）敷き詰めてできる形の様子を調べる。
2. 分度器で４つの角の大きさを測ってそれらの和を求める。
3. 四角形の４つの角を切り取りって寄せ集める。
４ 事例２ 結果を類推する
長方形や正方形の四つの角の大きさの和が３６０°であるから一般の四角形も３６０°であろうと考えるのは類推的な考え方です。
結果の見通しをもつ：結果を類推する
【問題】「四角形の４つの角の大きさの和について調べましょう。」
類似した既習の図形を思い出す
既知の事項
「四角形の仲間の長方形と正方形の４つの角の大きさの和について調べましょう。」
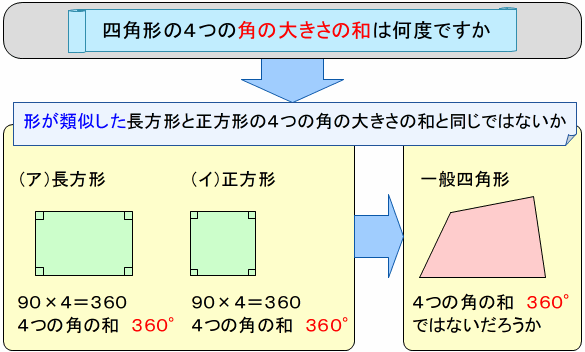長方形や正方形の角は，それぞれ直角で，角の大きさは９０°です。したがって４つの角の和は，３６０°です。
類推的な考え方
長方形や正方形は特殊ですが，一般四角形と形が類似しています。それらの図形の４つの角の和は，３６０°であるから，一般四角形の角の和も３６０°になるだろうと類推できます。
５ 事例３ 方法と結果を類推する
帰納的な考え方で，３のだんの九九を構成した後，続いて４のだんの九九を構成します。
３のだんを構成するときに見出した「３のだんの九九のきまり：かける数が１ふえると答えは３ずつふえる」を基にして，４のだんの九九の構成の方法と結果を考えます。これは，類推的な考え方です。
方法と結果の見通しをもつ：方法と結果を類推する
【問題】「４のだんの九九のつくり方を調べましょう。」
類似した既習の九九を思い出す
既知の事項
【問題】３のだんの九九をつくる
共通するきまりや性質を見つける
３×１＝３
３×２＝（３）＋３＝６
…
「かける数が１ふえると答えは３ずつふえること」が，３×５，３×６などでも成り立つだろう
きまりを使って答えを求める
３×５＝１２＋３＝１５，３×５＝３＋３＋３＋３＋３＝１５ となり正しい。
３×６＝１５＋３＝１８，３×６＝３＋３＋３＋３＋３＋３＝１８ となり正しい。
…
３のだんは，「かける数が１ふえると答えは３ずつふえる」ことが分かった。
類推的な考え方
４のだんも，３のだんと似た決まりがあるのではないか。
４のだんは，「かける数が１ふえると答えは４ずつふえる」のではないか。
類似した３のだんの九九の構成の方法を基にして４のだんの九九を考える。
【問題】「４のだんの九九をつくりましょう」
３のだんと同じように，共通するきまりや性質を見つけます
４×１＝３
４×２＝（４）＋４＝８ かける数が１ふえて２になると，答えは４ふえて ８になる
４×３＝（４＋４）＋４＝１２ かける数が１ふえて３になると，答えは４ふえて１２になる
きまりは「かける数が１ふえると答えは４ずつふえること」になりそう。３のだんと似ている。
もう一つ調べよう。
４×４＝（４＋４＋４）＋４＝１６ かける数が１ふえて４になると，答えは４ふえて１６になる
３のだんと同じ方法でできそうだ。
６ まとめ
小学校算数科で育成する数学的な考え方の「類推的な考え方」は，既習の内容との類似性に着目して新しい事柄を見いだす考え方です。
ある事柄Ａについて，その性質，法則または解決の方法を知りたい。しかし，それがわからないというとき，Ａと似よりの既知の事柄Ａ’を思い出し，（Ａ’については性質や法則，解決の方法などＰ’が分かっているとする），ＡについてもＡ’のＰ’と同様なことが言えるのでないかというように思考を進めていこうと努めるものです。
類推的な考え方は，見通しをもったり，根拠を説明したりするときに用いられます。
特に，解決の方法と結果の見通しをもつときに，しばしば活用されます。
＊１ 引用文献 片桐重男 数学的な考え方とその指導第１巻「数学的な考え方の具現化と指導」明治図書２００４年
＊２ 参考文献
文部科学省小学校学習指導要領解説算数（1）第1章～第2章（平成20年6月）[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2009/06/16/1234931_004_1.pdf（参照2017/05/16）
文部科学省小学校学習指導要領解説算数（2）第3章～第4章（平成20年6月）[ONLINE]http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2009/06/16/1234931_004_2.pdf（参照2017/05/16）
＊３ 啓林館 わくわく算数２下平成２７年度版
＊４ 参考文献 片桐重男 数学的な考え方・態度とその指導１「数学的な考え方の具現化」明治図書１９８８年
