|
1 ソフト名 小学校算数科5年「体積」表面積では比べられない
サイズ:807 KBytes ファイル名:taiseki-surface-area.exe 作成者:Marche 種別:フリーソフト
確認済動作環境:WindowsVista,Windows10
2 ソフトの概要
本教材ソフトは,単元「体積」の導入時に,児童の実態など必要に応じて活用するものです。
体積が表面積で比べられないことに実感をもった理解を促したいときに活用できます。
本ソフトを使用する単元の指導のねらいや指導のポイントについては,本サイト別稿の「算数科5年「体積」導入・発展教材ソフトを使った授業」を参照して下さい。

3 本ソフト使用上のポイント
(1)直方体の体積は,表面積で測れるのかを視点に話合いを焦点化
4年生の学習で,周りの長さが同じ長方形と正方形の広さを比べる場面があります。
縦3cm,横5cmの長方形と一辺が4cmの正方形では,周りの長さはともに16cmです。
これらの面積を比較するとき,周りの長さが同じことから,面積は同じと考える児童がいます。
体積を比較する場合も,似たつまずきが見られることがあります。
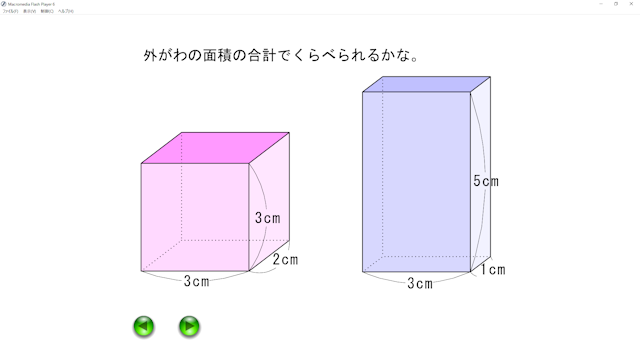
本ソフトでは,縦2cm,横3cm,高さ3cmの直方体(以下直方体アとする)と縦1cm,横3cm,高さ5cmの直方体(以下直方体イとする)の体積を比べる問題場面を設定しています。
本ソフトでは,提示する2つの直方体の表面積と体積は,それぞれ以下のようになります。
表面積
直方体ア…(2×3)×4+(3×3)×2=42 表面積42cm2
直方体イ…(3×1)×2+(5×3)×2+(1×5)×2=46 表面積46cm2
直方体ア<直方体イ
となり,表面積は,直方体イの方が広いことになります。
体積
直方体ア…2×3×3=18 体積18cm3
直方体イ…1×3×5=15 体積15cm3
直方体ア>直方体イ
となり,体積は,直方体アの方が大きいことになります。
このように本教材ソフトでは,二つの直方体の体積は,表面積で測れたり比べられたりできるのかという視点で話合いを焦点化できます。
(2)二つの直方体の体積は,表面積では比べられないことに気付く話合いを設定する
これらの直方体のかさ・体積を比較する場面では,次のような児童のつまずきが考えられます。
- 測定対象の量が,3次元の量であり立体であることに気付いていない。すなわち,平面と考えている。
- 測定対象の量(かさ,体積)は,表面積に置き換えて比べられると考えている。
このようなつまずきが想定される中,本ソフトを活用するなどして体積の意味について児童が考え話し合うことで,体積は表面積で比べられないことを見出すことが期待できます。
次期学習指導要領では,主体的・対話的で深い学び(「アクティブ・. ラーニング」)の視点からの学習過程の改善が求められます。
このような問題場面をつくるなどしてその実現につなげることが大切です。
| 算数科5年「体積」で,次のつまずきが見られるとき,本教材ソフトを活用するなどして,体積は表面積で比べられないことを話し合うようにする。 ・測定対象の量が,3次元量であることに気付いていない。 ・体積は,表面積に置き換えて比べられると考えている。 話合いでは,次の点が大切である。 (1)直方体の体積は,表面積で測れるのかという点に話合いを焦点化する (2)二つの直方体の体積は,表面積では比べられないことに気付く主体的・対話的で深い学びとなる話合いを設定する |